3.2.4. Правила Кирхгофа

Эти правила были сформулированы Кирхгофом в 1847 году, они используются для расчета разветвленных цепей постоянного и квазистационарного тока - цепей, содержащих несколько замкнутых контуров. Если записать закон Ома (3.22) для замкнутой цепи (для нее начальная и конечная точки совпадают, т.е. ), то из него следует второе правило Кирхгофа

(3.92)

Второе правило Кирхгофа формулируется следующим образом: алгебраическая сумма падений напряжения на разных участках замкнутой цепи равна алгебраической сумме э.д.с., действующих в этой цепи. Число независимых уравнений (ни одно из них не является следствием других), которые можно записать по второму правилу, равно числу замкнутых контуров (цепей), которые нельзя получить наложением одного на другой. Так, для схемы, приведенной на рис.3.5,а, число независимых уравнений равно двум, один из трех контуров получается наложением двух других.

Рис.3.36

Рассмотрим выбор знаков в формуле (3.23). Для этого сначала произвольно выбирают направление токов на разных участках разветвленной цепи и направление обхода замкнутых контуров (цепей). Если направление тока совпадает с направлением обхода контура, то тогда для силы тока выбирается знак плюс («+»), если нет – знак «-». Если э.д.с. источника тока в направлении обхода контура повышает свой потенциал (происходит переход от отрицательного полюса источника к его положительному полюсу), то для нее в уравнениях (3.23) выбирается знак плюс, если нет – знак минус.

Для приведенной на рис.3.36,а схемы по второму правилу Кирхгофа можно записать два уравнения:

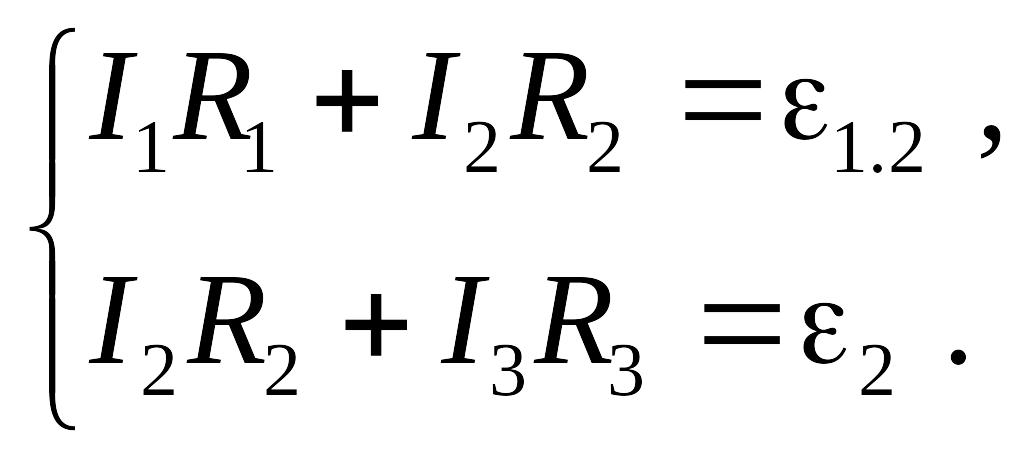
Для формулировки первого правила Кирхгофа введем понятие узла электрической цепи. Узел электрической цепи - это точка цепи, в которой сходятся три или более проводников. Тогда из закона сохранения электрического заряда ( он не может накапливаться в какой-либо точке цепи) следует первое правило Кирхгофа

(3.93)

согласно которому алгебраическая сумма токов, сходящихся в узле равна нулю.

Принято брать силу тока I со знаком «+», если ток входит в узел, и со знаком минус “-“, если ток выходит из узла. Число независимых уравнений, которые можно записать по этому правилу, равно числу узлов разветвленной цепи минус один. Так, для цепи, приведенной на рис.3.36,а, можно записать только одно уравнение, например, для узла б

Система уравнений (3.92) и (3.93) позволяет провести расчет электрических цепей при различных исходных данных. Для разветвленной цепи, содержащей большое число контуров, для решения системы уравнений необходимо использовать известный в алгебре метод определителей.

В качестве примера рассмотрим, что измеряет вольтметр, подключенный к электрической цепи, содержащей источник тока с э.д.с. и сопротивлением r, сопротивление R внешней части цепи и ключ К (рис.3.36,б).

Сопротивление вольтметра выбирают значительно бóльшим сопротивлений, включенных в электрическую цепь (RV>>R,r), поэтому подключение вольтметра не оказывает существенного влияния на протекание тока в различных частях цепи.

Пусть ключ К замкнут (рис.3.36,б). Составим уравнения закона Ома для участков цепи 1-3-2, 2-4-1 и 2-5-1 (обход участка начинается с первой точки). Используя формулу (3.19) и правило выбора знаков получим:

;(3.94а)

(3.94б)

(3.94в)

Из уравнения (3.94б) следует, что вольтметр измеряет разность потенциалов на участке цепи 1-2 (1-3-2,2-4-1,2-5-1), к которому он подсоединен, а не напряжение на этом участке.

Уравнения (3.94а) и (3.94б) дают следующие равенства;

(3.95)

т.е. напряжение, измеряемое вольтметром, равно напряжению на участках цепи 1-3-2 и 2-5-1, т.к. они подключены параллельно друг к другу, а они в свою очередь равны разности потенциалов на этих участках.

В соответствии с правилами Кирхгофа можно записать два независимых уравнения для двух контуров 1-3-2-4-1 и 1-3-2-5-1 и одно уравнение для узла 2.

(3.96а)