3.2.2. Закон Ома для однородного участка цепи. Закон Джоуля-Ленца

Однородным участком электрической цепи называют участок, на котором направленное движение зарядов происходит под действием только кулоновских сил. Для него Г. Ом в 1826 году экспериментально установил следующий закон (закон Ома): сила тока I, текущего по однородному участку цепи, прямо пропорциональна напряжению U, приложенному к нему, и обратно пропорциональна сопротивлению R этого участка цепи

(3.75)

Отметим, что в данном случае напряжение U совпадает с разностью потенциалов между начальной и конечной точками участка

(см. параграф 3.3).

На основе формулы (3.75) вводится понятие сопротивления R однородного участка цепи: сопротивление R характеризует свойство проводника препятствовать протеканию по нему электрического тока и равно

(3.76)

Сопротивление R однородного участка цепи не зависит не от U, не от I, но определяется геометрическими размерами проводника, его материалом и температурой.

Вольт-амперной характеристикой (ВАХ) однородного участка цепи называют график зависимости силы тока I от приложенного к нему напряжения (рис.3.2,а); он представляет собой прямую линию, угол наклона которой определяет электрическое сопротивление участка (рис.3.33,а).

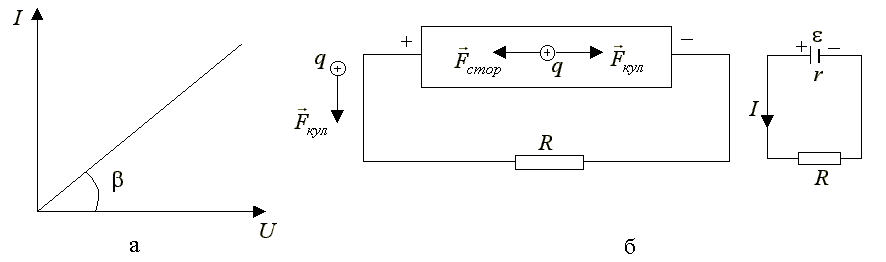
Рис.3.33

На практике обычно используют проводники цилиндрического вида длиной l и площадью поперечного сечения S. Это позволяет ввести новую характеристику - удельное сопротивление  проводника по следующей формуле:

(3.77)

Удельное сопротивление проводника зависит только от его материала и температуры. Оно численно равно сопротивлению R проводника при l=1 м и S=1 м2.

Для чистых металлических проводников в области комнатных температур удельное сопротивление практически линейно возрастает с повышением температуры, а именно:

(3.78)

где - удельное сопротивление проводника при температуре ;

t – температура проводника по шкале Цельсия.

Входящий в формулу параметр называют температурным коэффициентом сопротивления (ТКС), он численно равен относительному изменению удельного сопротивления проводника при повышении температуры проводника на :

(3.79)

Зависимость сопротивления R металлического проводника также соответствует формуле (3.78), так как размеры проводника (l,S) обычно изменяются с температурой значительно слабее, чем удельное сопротивление проводника:

(3.80)

Рис.3.34

Для чистых металлов ТКС является положительной величиной, примерно равной К-1. При низких температурах, когда колебания положительных ионов кристаллической решетки не оказывают существенного влияния на движение свободных электронов, удельное сопротивление не изменяется с температурой, оставаясь постоянной величиной (рис.3.34, график 1).

Для многих металлов при определенной температуре (ее называют температурой перехода в сверхпроводящее состояние, ) сопротивление R металла обращается в ноль (R=0), металл при Т< будет находиться в сверхпроводящем состоянии (рис.3.34, график 2).

Для использования в практических целях необычных свойств сверхпроводящего состояния необходимо создавать материалы с высокими значениями температуры (комнатные температуры и выше). На этом пути в 1968 г. для металлооксидных соединений были получены = (70-120) К, это открытие получило название явления высокотемпературной сверхпроводимости.

Отметим, что ТКС может и уменьшаться с повышением температуры ( <0). Это, например, наблюдается для растворов электролитов и для полупроводников, что связано с увеличением в них концентрации свободных носителей заряда при повышении температуры.

В заключение этого параграфа выведем формулу для расчета количества теплоты Q, выделяемого в проводнике при протекании по нему электрического тока. Если в магнитном поле проводника с током отсутствует перемещение других тел (заряженных частиц других проводников с током) и не изменяется химический состав проводника (нет электролиза), то тогда работа сил электрического поля по перемещению заряда в проводнике целиком расходуется на выделение теплоты.

В этом случае количество теплоты dQ , выделяемое за малый промежуток времени dt, можно рассчитать таким образом

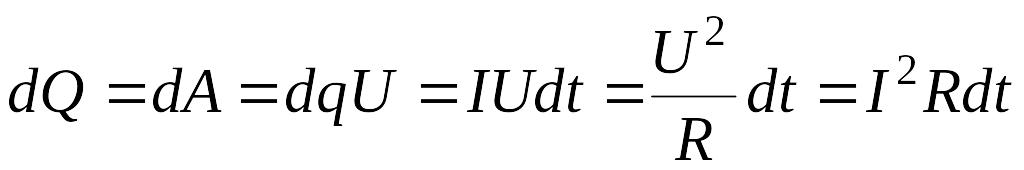(3.81)

Для конечного промежутка времени в случае переменного тока получим:

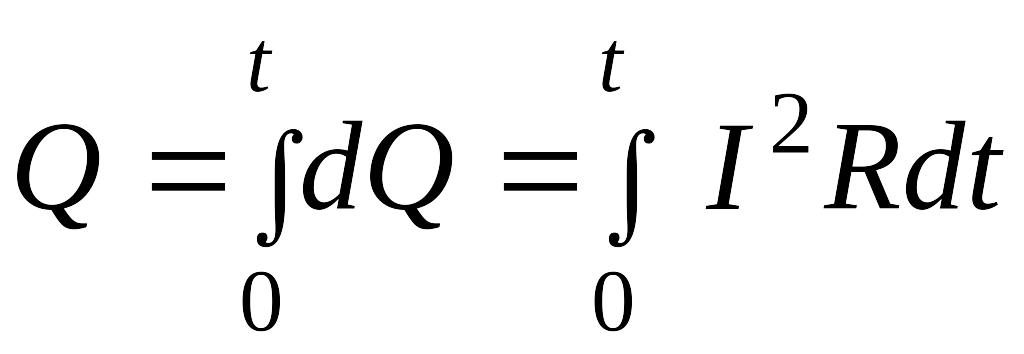(3.82а)

а для постоянного тока (I=const)

(3.82б)

Формула (3.81) получила название закона Джоуля - Ленца. Он формулируется следующим образом: количество теплоты, выделяемое в проводнике при протекании по нему электрического тока равно произведению квадрата силы тока на сопротивление проводника и на время протекания по нему тока.