3.1.12.4. Неполярный диэлектрик во внешнем электрическом поле

Во внешнем электрическом поле происходит смещение зарядов неполярных молекул, они становятся диполями и приобретают индуцированные дипольные моменты. На рис.2.24 показано расположение молекул-диполей на поверхности и внутри диэлектрика, представляющего собой прямоугольную пластину длиной l и площадью поперечного сечения S, во внешнем однородном электрическом поле напряженности .

Из рисунка видно, что внутри происходит компенсация зарядов соседних молекул (суммарный заряд, заключенный в областях, ограниченных замкнутыми пунктирными линиями, равен нулю). Некомпенсированными остаются заряды молекул на противоположных гранях диэлектрика, они называются связанными зарядами, поскольку эти заряды находятся внутри молекул и не могут свободно перемещаться по всему объему диэлектрика (рис.3.24).

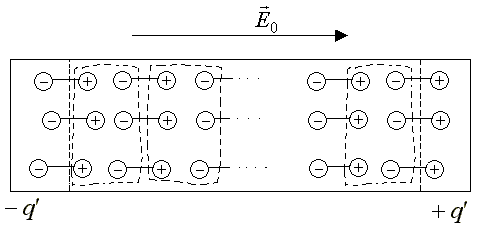
Рис.3.24

Из рис.3.24 можно получить несколько упрощенных схем диэлектрика (рис.3.25), что позволяет провести простой вывод ряда формул. Некоторые из них приводятся ниже.

1. Электрическое поле диэлектрика эквивалентно электрическому полю плоского конденсатора с поверхностной плотностью заряда его пластин, равной (рис.3.25,а). Следовательно,

(3.64)

2. Диэлектрик подобен большой полярной молекуле (рис.3.25,б). Поэтому поведение диэлектрика во внешнем электрическом поле подобно поведению диполя. Рассчитаем модуль вектора поляризации:

(3.65)

Рис.3.25

где - проекция вектора на направления нормали к поверхности диэлектрика (рис.3.25,в, = для правой грани).

3.Все индуцированные дипольные моменты молекул направлены вдоль линии , также направлен и вектор поляризации (рис.3.25,в). Учитывая выражения (3.64) и (3.65), можно вывести формулу (3.60)

3.1.12.5. Полярный диэлектрик во внешнем электрическом поле

В отсутствие электрического поля за счет теплового движения молекул их дипольные моменты разбросаны хаотично по все направлениям, следовательно, диэлектрик неполяризован и вектор поляризации равен

нулю (рис.3.26,а)

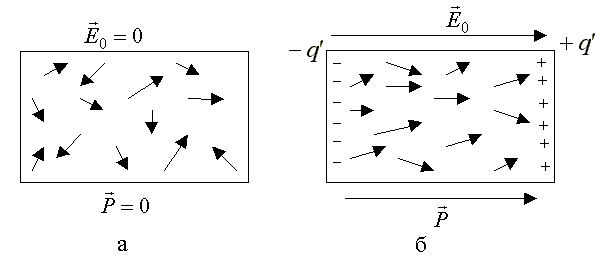
Рис.3.26

Во внешнем электрическом поле его силы стремятся установить дипольные моменты молекул вдоль линий , чему препятствует тепловое движение молекул. За счет действия этих двух факторов наблюдается преимущественная ориентация дипольных моментов молекул вдоль поля (рис.3.26,б). Поэтому за счет поворота молекул диэлектрик поляризуется ( ), поляризация сопровождается появлением связанных зарядов на противоположных гранях диэлектрика.

Все это свидетельствует о том, что поведение такого диэлектрика во внешнем электрическом поле подобно поведению диэлектрика из неполярных молекул, а следовательно, и поведению диполя.

3.1.12.6. Физический смысл теоремы Гаусса для вектора электрического смещения и для вектора поляризации

Учитывая формулы (3.29) и (3.63) запишем

(3.66)

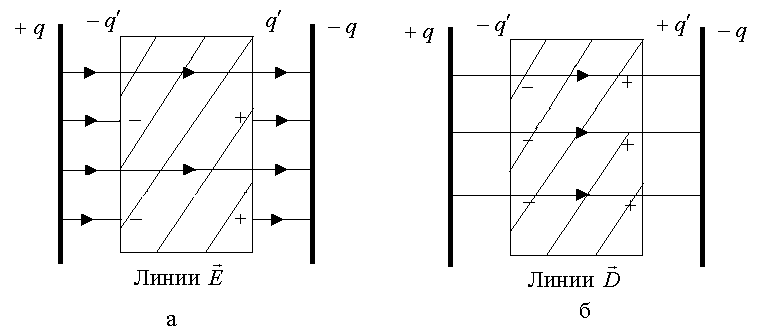
Рис. 3.27

Из уравнения (3.66) следует, что источником вектора являются свободные заряды и поэтому линии на границе диэлектрика, где появляются связанные заряды , не прерываются. Поэтому является удобным графически изображать электрическое поле в присутствии диэлектрика с помощью линий . На рис.3.27 в качестве примера приведено графическое изображение с помощью линий и электрического поля плоского конденсатора, внутри которого находится прямоугольная пластина из диэлектрика с относительной диэлектрической проницаемостью .

Выведем формулы, связывающие свободные заряды и их поверхностную плотность на пластинах конденсатора со связанными зарядами и их поверхностной плотностью на диэлектрике. Для этого запишем для модуля напряженности электрического поля внутри пластины (рис.3.27,а) формулы в соответствии с выражениями (3.57), (3.58), (3.64)

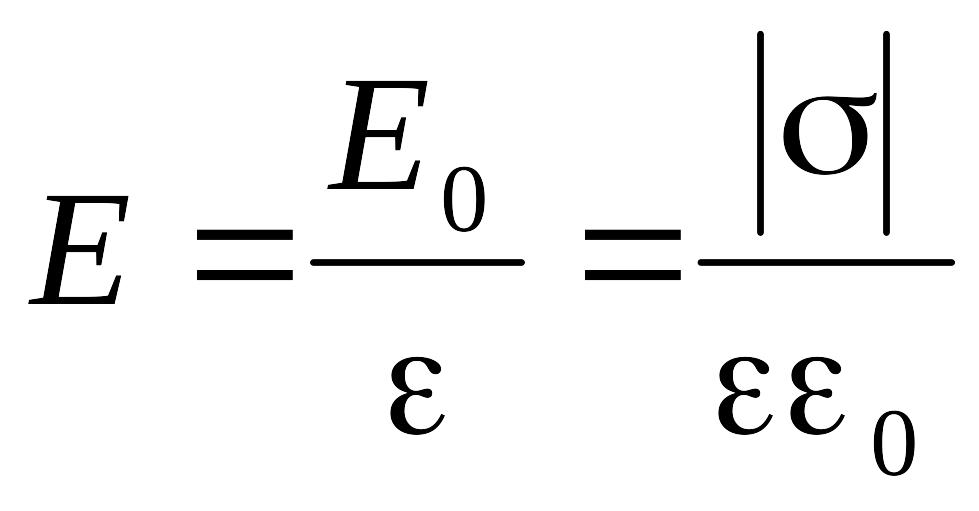
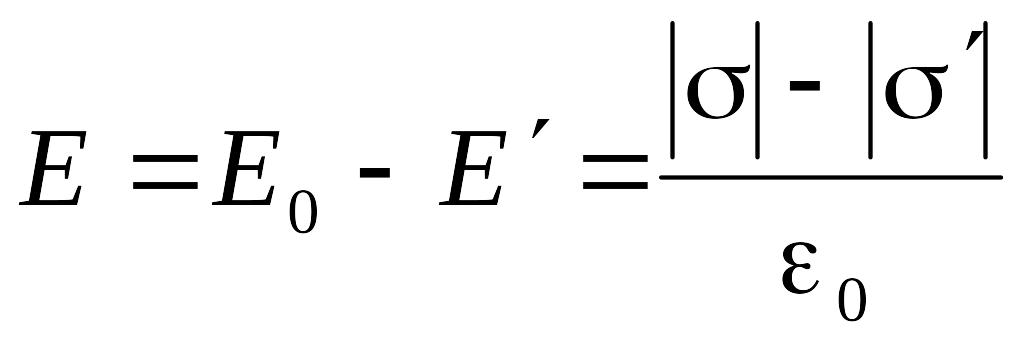
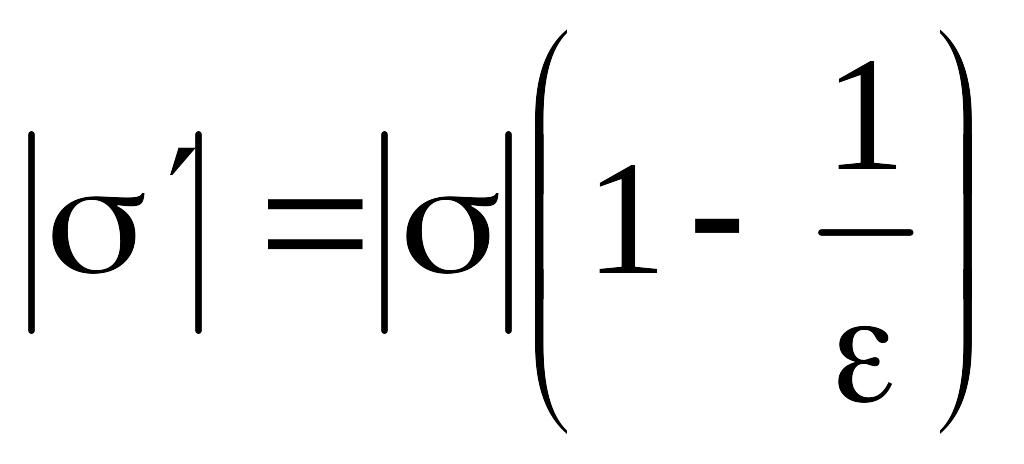(3.67)

(3.68)

В формуле (3.68) явно не выделены знаки зарядов и , они могут быть как больше, так и меньше нуля, но если , то тогда , и наоборот (это соответствует факту ослабления внешнего поля внутри диэлектрика).

Выражение (3.68) было использовано в параграфе 3.1.7 для выяснения физического смысла теоремы Гаусса для вектора электростатического поля, а именно, источником вектора являются свободные и связанные заряды. Поэтому часть линий на границе диэлектрика прерываются и могут изменять свое направление. Из двух векторов и , описывающих электростатическое поле, вектор является истинным вектором этого поля, так как источником являются все существующие в природе электрические заряды, а вектор - вспомогательный вектор.

Для вектора поляризации в соответствии с формулами (3.62), (3.66) и (3.68) получим

(3.69)

т.е. источником вектора являются связанные заряды.