3.1.12.2. Поведение диполя в электрическом поле

1. Однородное электрическое поле. На заряды диполя в однородном электрическом поле действует пара одинаковых по модулю сил ( ), вызывающих вращение диполя вокруг его центра (точки О) с уменьшением угла между дипольным моментом и вектором (рис.3.22,а).

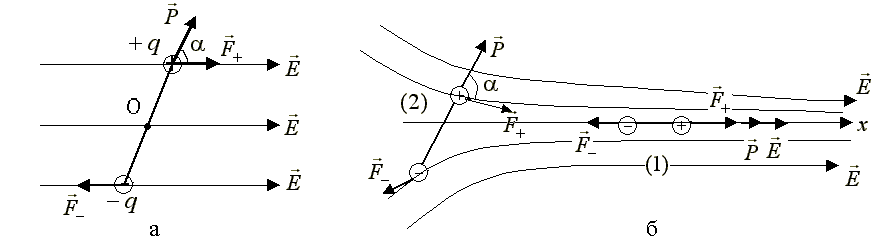
Рис.3.22

В итоге диполь установится в положении, для которого угол между векторами и будет равен нулю ( , , положение устойчивого равновесия).

Введем потенциальную энергию диполя W в электрическом поле. Для этого рассчитаем работу сил поля по вращению диполя от состояния 1, при котором угол , до состояния 2 ( ).

Используя формулу для работы силы по вращению тела, получим:

(3.54)

При выводе формулы (3.54) было учтено, что силы электростатического поля являются консервативными, поэтому их работа равна убыли потенциальной энергии диполя в этом поле.

Из выражения (3.54) видно, что в положении устойчивого равновесия потенциальная энергия диполя минимальна и равна .

2. Неоднородное электрическое поле. Пусть электрическое поле нарастает вдоль оси Ох (рис.3.22,б). Если угол между векторами и равен нулю (положение 1), то тогда под действием пары сил диполь будет втягиваться в область более сильного поля ( , рис.3.22,б). При начальном угле (положение 2) пара сил, действующих на заряды диполя, будет приводить к его вращению с уменьшением угла и втягиванию в область более сильного поля, т.е. к поступательному движению вдоль оси Ох. При начальном угле диполь будет сначала поворачиваться с уменьшением угла и выталкиваться в область более слабого поля. При достижении угла он поворачивается с уменьшением угла и начинает втягиваться в область более сильного поля.

Можно записать формулу для проекции на ось Ох силы , вызывающей поступательное движение диполя, используя известное из механики выражение , связывающее консервативную силу и потенциальную энергию

(3.55)

Итак, при любом начальном угле  диполь в неоднородном электрическом поле в итоге втягивается в область более сильного поля. Такое поведение диполя используется в пылеулавливателях. В какой-либо части трубы, из которой выходит дым (это могут быть, например, побочные газообразные продукты горения на тепловых электростанциях, металлургического производства различных металлов), создается неоднородное электрическое поле. Частицы дыма (они представляют собой диполи) втягиваются в область более сильного поля и не попадают в воздушную атмосферу, не загрязняют окружающую среду.

3.1.12.3 Характеристики, вводимые для описания электрического поля в присутствии диэлектриков

1. Диэлектрик, помещенный во внешнее электрическое поле напряженности , поляризуется, т.е. создает свое собственное электрическое поле напряженности . При этом напряженность результирующего электрического поля будет равна

(3.56)

Поляризация диэлектрика сопровождается появлением на его противоположных гранях некомпенсированных связанных зарядов , которые и создают поле . Поверхностная плотность заряда характеризует распределение заряда. по поверхности диэлектрика.

2. Относительная диэлектрическая проницаемость среды. Она показывает, во сколько раз модуль напряженности поля в вакууме больше модуля напряженности поля внутри диэлектрика

(3.57)

Эта формула справедлива для однородного изотропного диэлектрика, заполняющего все пространство или представляющего собой цилиндрические, сферические и прямоугольные пластины, находящиеся соответственно в электрическом поле осевой или сферической симметрии или в однородном поле. Тогда между векторами и угол будет равен 1800 и можно записать

(3.58)

В зависимости от формы диэлектрика и его расположения во внешнем электрическом поле угол между векторами и может изменяться (рис.3.23), но всегда внутри диэлектрика электрическое поле связанных зарядов ослабляет внешнее электрическое поле ( , рис.3.23 точки 1 и 4), чего нельзя сказать о суммарном электрическом поле за пределами диэлектрика (ЕЕ0, рис.3.23 точка 3; ЕЕ0, рис.3.23 точка 2).

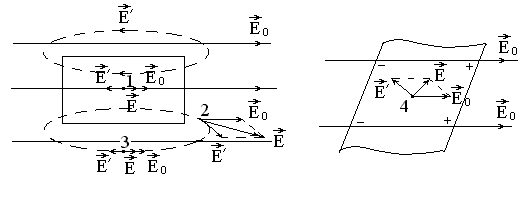
Рис.3.23

3. Вектор поляризации (поляризованность) . Он равен векторной сумме дипольных моментов молекул единицы объема диэлектрика.

(3.59)

Вектор поляризации описывает способность диэлектрика создавать свое собственное поле . Можно показать, что

(3.60)

Из опыта известна формула

(3.61)

где величина называется диэлектрической восприимчивостью диэлектрика.

4. Вектор электрического смещения (электрической индукции) . Он вводится по формуле

(3.62)

Используя формулу (3.60) можно записать

,

(3.63)