4. Класифікація задач і методів математичного програмування.

У математичному програмуванні виділяють два напрямки — детерміновані задачі і стохастичні. Детерміновані задачі не містять випадкових змінних чи параметрів. Уся початкова інформація повністю визначена. У стохастичних задачах використовується вхідна інформація, яка містить елементи невизначеності, або деякі параметри набувають значень відповідно до визначених функцій розподілу випадкових величин. Наприклад, якщо в економіко-математичній моделі врожайності сільськогосподарських культур задані своїми математичними сподіваннями, то така задача є детермінованою. Якщо ж врожайності задані функціями розподілу, наприклад нормального з математичним сподіванням а і дисперсією D, то така задача є стохастичною.

Якщо у відповідних економічних процесах випадкові явища не відіграють істотної ролі, то задачу можна розв’язувати як детерміновану. У іншому разі адекватна економіко-математична модель має бути стохастичною, тобто містити випадкові функції та величини. Структура та розв’язування таких задач вивчаються в окремому розділі, який називається стохастичним програмуванням.

Як детерміновані, так і стохастичні задачі можуть бути статичними (однокроковими) або динамічними(багатокроковими).

Задачі математичного програмування поділяють також на дискретні і неперервні. Дискретними називають задачі, в яких одна, кілька або всі змінні набувають лише дискретних значень. З-поміж них окремий тип становлять задачі, в яких одна або кілька змінних набувають цілочислових значень. Їх називають задачами цілочислового програмування. Якщо всі змінні можуть набувати будь-яких значень на деяких інтервалах числової осі, то задача є неперервною.

Оскільки в економіко-математичних моделях залежності між показниками описані за допомогою функцій, то відповідно до їх виду всі вище згадані типи задач поділяють на лінійні та нелінійні.

Найпростішими з розглянутих типів є статичні, детерміновані, неперервні та лінійні задачі. Важливою перевагою таких задач є те, що для їх розв’язування розроблено універсальний метод, який називається симплексним методом. Теоретично кожну задачу лінійного програмування можна розв’язати. Для деяких типів лінійних задач, що мають особливу структуру, розробляють спеціальні методи розв’язання, які є ефективнішими. Наприклад, транспортну задачу можна розв’язати симплексним методом, але ефективнішими є спеціальні методи, наприклад, метод потенціалів.

Як окремий тип розглядають дробово-лінійне програмування, коли обмеження є лінійними, а цільова функція — дробово-лінійна. Особливий тип становлять задачі теорії ігор, які широко застосовуються в ринковій економіці. Адже тут діють дві чи більше конфліктних сторін, які мають частково або повністю протилежні цілі. У сукупності задач теорії ігор, у свою чергу, також виокремлюють певні підтипи. Наприклад, ігри двох осіб із нульовою сумою.

5. Цільова функція задачі лп. Система лінійних обмежень та її геометрична інтерпретація.

Загальна модель задачі математичного програмування має такий вигляд:

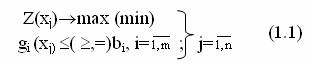
У структурі моделі (1.1) можна виділити 3 елементи:

1) Набір керованих змінних x1, x2, ... x n, значення яких підлягають оптимізації. Різні допустимі комбінації значень змінних відповідають можливим розв’язкам задачі.

2) Цільова функція z (x1, x2, ... x n) - функція, що виражає залежність прийнятого критерію оптимальності від керованих змінних.

Критерій оптимальності є мірою наближення розв’язку до поставленої мети. В економічних задачах, як правило, таким критерієм виступає показник ефективності функціонування системи (наприклад, прибуток від реалізації продукції, продуктивність праці, таке інше) або показник витрат. Слід зазначити, що одній меті можуть відповідати декілька критеріїв оптимальності (багатокритеріальна задача); в цьому разі цільова функція має враховувати всі виділені критерії.

3) Умови або обмеження g (x1, x2, ... x n), що накладаються на значення змінних або на співвідношення між ними.

Розглянемо на площині Х10x2 сумісну систему лінійних нерівностей:

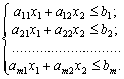 (2.9)

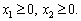
Кожна нерівність цієї системи геометрично визначає півплощину з граничною прямою ai1x1 +ai2x2 = bi(i = 1, 2, ...,т). Умови невід’ємності змінних визначають півплощини з граничними прямими х1 = 0 та х2 = 0. Система сумісна, тому півплощини як опуклі множини, перетинаючись, утворюють спільну частину, що є опуклою множиною і являє собою сукупність точок, координати кожної з яких є розв’язком даної системи (рис. 2.1).

Сукупність цих точок (розв’язків) називають багатокутником розв’язків, або областю допустимих планів (розв’язків) задачі лінйного програмування. Це може бути точка (єдиний розв’язок), відрізок, промінь, багатокутник, необмежена багатокутна область.

Якщо в системі обмежень (2.9) буде три змінних, то кожна нерівність геометрично визначатиме півпростір тривимірного простору, граничними площинами котрого будуть ai1x1 + ai2x2 + ai3x3 = bi(i = 1, 2, ...,т), а умови невід’ємності — півпростори з граничними площинами хj = 0 (j = 1, 2, 3), де і — номер обмеження, а j — номер змінної. Якщо система обмежень сумісна, то ці півпростори як опуклі множини, перетинаючись, утворять у тривимірному просторі спільну частину, що називається багатогранником розв’язків. Він може бути точкою, відрізком, променем, багатокутником, багатогранником, багатогранною необмеженою областю.

Нехай у системі обмежень (2.9) кількість змінних більша, ніж три: х1, х2,… хn; тоді кожна нерівність визначає півпростір n-вимірного простору з граничною гіперплощиною аi1x1 + ai2x2 + ai3x3 + … +ainxn = bi(i = 1, 2, ...,т). Кожному обмеженню виду (2.9) відповідають гіперплощина та напівпростір, який лежить з одного боку цієї гіперплощини, а умови невід’ємності — півпростори з граничними гіперплощинами хj = 0 (j = 1, 2, 3, ..., n).

Якщо система обмежень сумісна, то за аналогією з тривимірним простором вона утворює спільну частину в n-вимірному просторі — опуклий багатогранник допустимих розв’язків.

Отже, геометрично задача лінійного програмування являє собою відшукання координат такої точки багатогранника розв’язків, при підстановці яких у цільову лінійну функцію остання набирає максимального (мінімального) значення, причому допустимими розв’язками є усі точки багатогранника розв’язків.

Цільову функцію

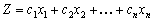
в п-вимірному просторі основних змінних можна геометрично інтерпретувати як сім’ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z.. Допустимий та оптимальний розв’язки задачі ЛП, властивості розв’язків.

Допустимий розв’язок – це такий впорядкований набір чисел з х̄_д = (х₁⁰, х₂⁰), який задовольняє усі без винятку нерівності системи.

Область допустимих розв’язків – це сукупність усіх без винятку допустимих розв’язків задачі (це розв’язок системи обмежень).

Оптимальний розв’язок – це такий допустимий розв’язок, який дає найбільше або найменше значення цільової функції.

В задачах лінійного програмування оптимальні розв’язки завжди знаходяться на межі області допустимих розв’язків.

Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем.

Властивість 1. (Теорема 2.2) Множина всіх планів задачі лінійного програмування опукла.

Властивість 2. (Теорема 2.3) Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Властивість 3. (Теорема 2.4) Якщо відомо, що система векторів A1, A2, …, Ak (k ≤ n) у розкладі A1x1 +A2x2 + … + Anxn = A0, X ≥ 0 лінійно незалежна і така, що

A1x1 + A2x2 + … + Akxk = A0,

де всі xj ≥ 0, то точка X = (x1, x2, …, xk, 0, …, 0) є кутовою точкою багатогранника розв’язків.

Властивість 4. (Теорема 2.5) Якщо X = (x1, x2, …, xn) — кутова точка багатогранника розв’язків, то вектори в розкладі A1x1 + + A2x2 + … + Anxn = A0, X ≥ 0, що відповідають додатним xj, є лінійно незалежними.