
- •Сопротивление материалов – заочно Для студентов заочной формы образования Казанского государственного технологического университета
- •Примеры решения задач Задача 1. Стержневая система
- •Задача 2. Статически неопределимая стержневая система
- •Задача з. Теория напряженного состояния
- •Задача 4. Кручение
- •Задача 5. Геометрические характеристики плоских сечений
- •Задача 6. Плоский изгиб
- •Задача 8. Внецентренное сжатие
- •Задача 9. Изгиб с кручением
Задача 9. Изгиб с кручением
Шкив диаметром и с углом наклона ветвей
ремня к горизонту
![]() 1
делаетn оборотов в минуту и передает
мощностьN кВт. Два других шкива
имеют одинаковый диаметрD 2 и
одинаковые углы наклона ветвей ремня
к горизонту
1
делаетn оборотов в минуту и передает
мощностьN кВт. Два других шкива
имеют одинаковый диаметрD 2 и
одинаковые углы наклона ветвей ремня
к горизонту![]() 2
. Каждый из них передает мощностьN /2(рис.9.1).
2
. Каждый из них передает мощностьN /2(рис.9.1).
|
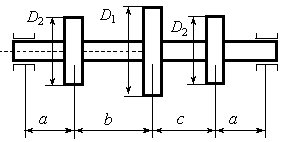
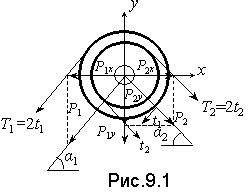
Требуется 1) определить моменты, приложенные к шкивам по данным величинам N иn ; 2) построить эпюру крутящих моментов M к ; 3) определить окружные усилия t 1 иt 2 , действующие на шкивы, по найденным моментам и заданным диаметрам шкивовD 1 иD 2 ; 4) определить давления на вал, принимая их равными трем окружным усилиям; 5) определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкива и вала не учитывать); 6) построить эпюры изгибающих моментов от горизонтальных сил М гор и от вертикальных силМ верт ;
7) построить эпюру суммарных моментов
8) по эпюрам М и иМ к найти опасное сечение и определить величину максимального расчетного момента по третьей теории прочности;
9) подобрать диаметр вала при [ |
Исходные данные: N = 40 кВт,n =
200 об/мин ,а =1,2 м,b = 1,6 м ,с =
1,0 м,D 1 = 1,2 м,D 2 = 0,68м,![]() 1
= 60 0 , ? 2 = 40 0 , [
1
= 60 0 , ? 2 = 40 0 , [![]() ]
= 70 МПа.
]
= 70 МПа.
Решение.
1. Определение моментов, приложенных к шкивам. Момент на шкивах по передаваемой мощности и скорости вращения вала определяется по формуле
![]() ,
,
где N - предаваемая валом мощность,
Вт,
![]() –
угловая скорость вращения вала, рад/с.
–
угловая скорость вращения вала, рад/с.
|
Угловую скорость можно вычислить по формуле |
|
|
Вычисляем момент на первом шкиве |
М 1 = 40·10 3 / 20,94 = 1947,2 Нм. |
Моменты на втором и третьем шкивах будут одинаковыми и равны половине момента первого шкива
![]() 973,6
Нм.
973,6
Нм.
|
|
2. Построение эпюры крутящих моментов. Так как подшипники вала крутящий момент не воспринимают, то на участках АВ иD К крутящий момент равен нулю. Участок А В :М к 1 = 0. Участок
ВС : Участок
С D : Участок
А В : По полученным значениям построим эпю py M к (рис.9.2.) |
3. Определение окружных усилий. Моменты на шкивах можно записать как разность окружных усилий, умноженную на радиус шкива, т.е. М = (Т -t )·D /2.
|
|
|
|
|
|
4. Рассчитываем усилия на вал от окружных
усилий
![]() ,
,![]() ,
,![]() и
и![]() :
:
|
|
|
5. Усилия Р 1 иР 2 спроектируем на координатные осих иу (см. рис.9.1):
|
|
Р 1х иР 2х действуют в горизонтальной плоскости и имеют противоположные направления.
Р 1у иР 2у действуют в вертикальной плоскости и имеют одинаковые направления. |
6. Построение эпюр изгибающих моментов от горизонтальных и от вертикальных сил.
а) Изгиб вала от горизонтальных сил (подшипники вала принимаются за шарнирные опоры).
Определение опорных реакций:
![]()
![]()
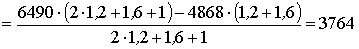 Н;
Н;
![]() ,
,
![]()
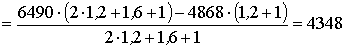 Н.
Н.
Проверяем правильность найденных реакций:
![]() .
.
|
|
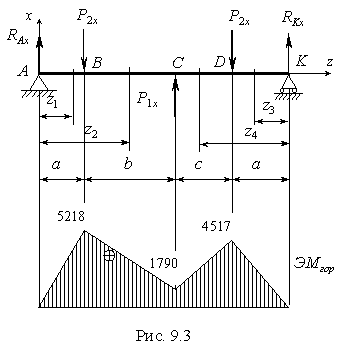
Для построения эпюры М гор рассмотрим каждый участок вала в отдельности(рис. 9.3). Участок
АВ
Участок
ВС
|
|
Участок KD
|
Участок DC
|
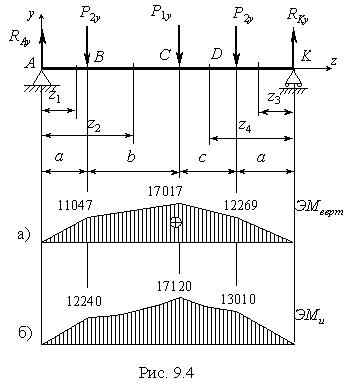
б) Изгиб вала от вертикальных сил (рис.9.4).
Определяем опорные реакции:
![]() ,
,
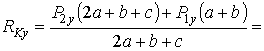
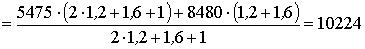 Н;
Н;
![]() ,
,
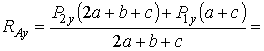
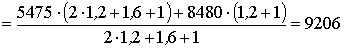 Н.
Н.
Проверяем полученные результаты
![]() .
.
Следовательно, реакции опор определены правильно.
Построение эпюры М верт.
|
Участок АВ
|
Участок ВС
|
|
Участок KD
|
Участок DC
|
|
|
По вычисленным значениям М верт в определенном масштабе строим эпюру(см. рис.9,4а). 7. Построение эпюры Ми По
значениям изгибающих моментов,
возникающих от вертикальной и
горизонтальной нагрузок, найдем
суммарный изгибающий момент
Вычислим значения М и на границах участков вала: На опорах М и = 0. В
точке В
В
точке С
В
точке D
|
По вычисленным значениям строим эпюру М и (рис. 9.4б).
8. Определение опасного сечения и величины максимального расчетного момента по третьей теории прочности.
Из эпюр М к иМ и видно, что
опасное сечение будет в точкеС ,
где![]() Нм,
Нм,![]() Нм.
Нм.
![]() Нм.
Нм.
9. Условие прочности вала по третьей
теории прочности определяется по формуле
 ,
,
где W x - осевой момент сопротивления
сечения. Для круга
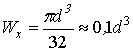 .
.
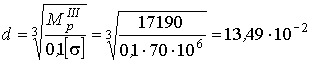 м.
м.
Принимаем d = 135 мм.
Литература: 1, §4.9.
![]()
Задача 12. УСТОЙЧИВОСТЬ
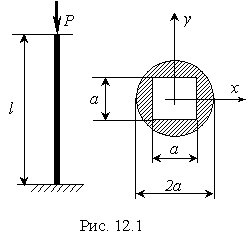
Стальной стержень длиной l = 2,3 м сжимается силойР = 300 кН. Условия закрепления стержня и форма его перечного сечения показаны на рис.(12.1).
|
|
Требуется найти: 1) размеры поперечного сечения стержня 2)
величину критической силы и коэффициент
запаса устойчивости при допускаемом
напряжении на сжатие
Решение. Определим основные геометрические характеристики сечения стержня. Главные моменты
инерции сечения
|

Площадь сечения

Минимальный радиус инерции
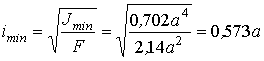
Расчет производим последовательными
приближениями, предварительно задавшись
значением коэффициента уменьшения
основного допускаемого напряжения
![]() .
Сечение будем считать подобранным
удовлетворительно, если действующее в
стержне напряжение? и допускаемое
напряжение на устойчивость
.
Сечение будем считать подобранным
удовлетворительно, если действующее в
стержне напряжение? и допускаемое
напряжение на устойчивость![]() отличаются
не более чем на 5%.
отличаются
не более чем на 5%.
В первом приближении задаемся![]() . Тогда из условия устойчивости
. Тогда из условия устойчивости![]() находим:
находим:
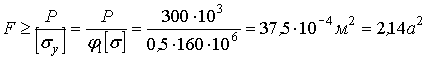
Отсюда
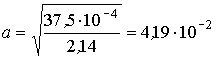 м,
м,
![]() м.
м.
Гибкость стержня
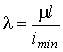 ,
,
где
![]() –
коэффициент приведения длины, величина
которого зависит от способа закрепления
стержня. Для стержня, защемленного с
одного конца
–
коэффициент приведения длины, величина
которого зависит от способа закрепления
стержня. Для стержня, защемленного с
одного конца![]() = 2.
= 2.
Тогда
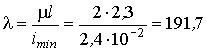 .
.
По значению
![]() из
таблицы для коэффициентов
из
таблицы для коэффициентов![]() найдем
соответствующее значение
найдем
соответствующее значение![]() :
:
при
![]() =
190
=
190![]() =
0,21,
=
0,21,
при
![]() =
200
=
200![]() =
0,19.
=
0,19.
Используя процедуру линейной интерполяции, получаем:
![]() .
.
Так как
![]() значительно
отличается от
значительно
отличается от![]() 1,
то повторим расчет с другим значением
1,
то повторим расчет с другим значением![]() .
.
В качестве второго приближения возьмем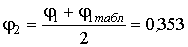 .
.
Тогда
 м
2 ,
м
2 ,![]() м,
м,
![]() м,
м, .
.
Из таблицы для коэффициента j подбираем:
![]() .
.
В третьем приближении принимаем
В третьем приближении принимаем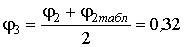 ,
,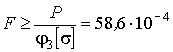 м
2 ,
м
2 ,![]()
м,
![]() м,
м,![]() .
.![]() .
.
Проверяем:
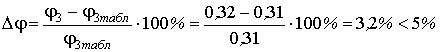 ,
что допустимо.
,
что допустимо.
Критическая нагрузка может быть вычислена:
при
![]() -
по формуле Эйлера:
-
по формуле Эйлера: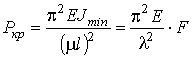 ,
,
при
![]() -
по формуле Ясинского:
-
по формуле Ясинского:![]() .
.
Для малоуглеродистых сталей предельная
гибкость
![]() =
100,
=
100,
а = 310 МПа,b =1.14 МПа,![]() МПа.
МПа.
В нашем случае![]() = 153,3 > 100. Следовательно, критическая
сила равна
= 153,3 > 100. Следовательно, критическая
сила равна
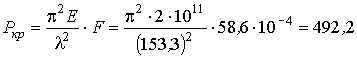 кН.
кН.
Коэффициент запаса устойчивости равен: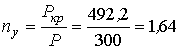 .
.
В заключение следует отметить, что в
большинстве случаев для достижения
удовлетворительного результата
достаточно двух-трех приближений. В тех
случаях, когда в первом приближении
получается слишком большая гибкость
(![]() > 200), можно порекомендовать в
качестве начального приближения принять
> 200), можно порекомендовать в
качестве начального приближения принять![]() =
0,1...0,2, либо воспользоваться приближенной
формулой для вычисления
=
0,1...0,2, либо воспользоваться приближенной
формулой для вычисления![]() :
:
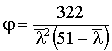 ,
где
,
где .
.
В частности, для малоуглеродистых сталей
![]() .
.
Литература: 1, гл.13; 2, гл.14.
![]()
Задача 15. СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ РАМА
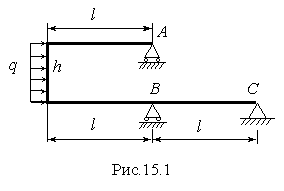
Для изображенной на рис.15.1 нагруженной в своей плоскости рамы, вертикальные элементы которой имеют моменты инерции J , а горизонтальные элементы –к J ;
|
|
Исходные данные: k = 1,5;l = 6 м,h = 3 м,q = 10 кН/м. Требуется: 1) установить степень статической неопределимости и выбрать основную систему; 2) написать канонические уравнения; 3) построить эпюры изгибающего момента от единичных сил и от заданной нагрузки; 4) найти коэффициенты канонических уравнений; 5) найти величины «лишних» неизвестных Х ; 6) выполнить деформационную проверку правильности определения неизвестных; 7) построить эпюры внутренних силовых факторов N ,Q y ,M x . |
Решение.
1. Степень статической неопределимости системы определяется равенством s =n – 3, где 3 – число независимых уравнений статики, которые можно составить для плоской системы сил;n – число связей, наложенных на раму. В нашем случаеs = 4 – 3 = 1.
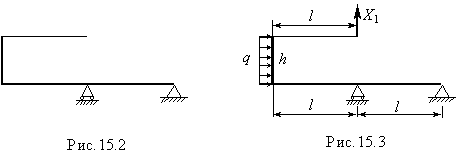
Для раскрытия статической неопределимости используем метод сил. Так называемую основную систему, получаемую из заданной статически неопределимой путем отбрасывания «лишних» связей, удобно выбрать, отбросив опору А (рис.15.2). Вариантов выбора основной системы может быть несколько. Следует остановиться на таком, при котором эпюры изгибающих моментов от заданных и единичных нагрузок будут наиболее простыми. Кроме того, основная система должна быть геометрически неизменяемой. Нельзя, например, отбрасывать ни горизонтальную, ни вертикальную связи в точкеС .
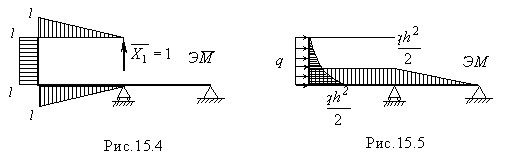
Прикладывая к основной системе неизвестную реакцию отброшенной опоры Х 1 и заданную нагрузкуq , получаем эквивалентную систему (рис. 15.3).
2. Каноническое уравнение метода сил для данной системы запишется в виде
![]() ,
(15.1)
,
(15.1)
где
d 11 - перемещение точкиА в направлении силыХ 1 от действия силыX 1 =1,
d 1 q - перемещение точкиА в направлении силыХ 1 от действия нагрузкиq .
|
|
|
|
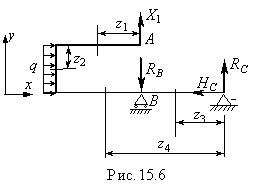
3. Строим эпюры изгибающего момента М отдельно от действия силыX 1 = 1 (рис.15.4) и нагрузкиq (грузовая эпюра) - рис.15.5. При этом в ряде случаев можно обойтись без определения опорных реакций.
4. Для отыскания коэффициентов канонического уравнения d 11 и d 1 q используем способ Верещагина.
Для определения коэффициента d 11 единичную эпюру М умножаем саму на себя:
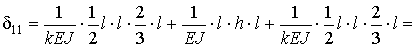
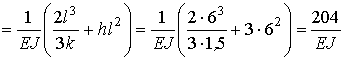 .
.
Для определения коэффициента d 1 q умножаем
грузовую эпюру М на единичную эпюру![]() :
:
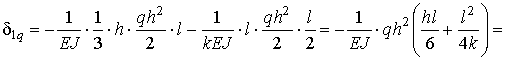
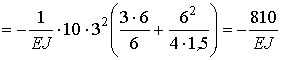 .
.
5. Из канонического уравнения (15.1) найдем неизвестную Х 1 :
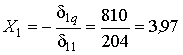 кН.
кН.
6. Из уравнений статики определяем опорные реакции (рис.15.6):
|
|
|
Сумма проекций всех сил на вертикальную ось у дает нуль, что подтверждает правильность определения опорных реакций:
![]() .
.
Составляем выражения для N ,Q y иМ x по участкам:
|
1
участок:
N 1 = 0;
|
2 участок:
|
|
3
участок:
|
4 участок:
|
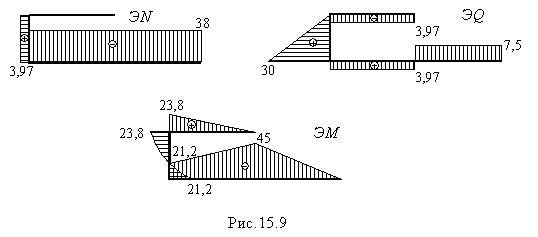
Вычислив значения внутренних усилий на границах участков, строим эпюры N ,Q y ,М x (рис.15.9).
Литература: 1, гл. 12; 2, гл, 6 .
![]()
Задача 16. ТОНКОСТЕННАЯ ОБОЛОЧКА
Тонкостенный цилиндрический резервуар
диаметром D = 6 м заполнен на высотуН = 14 м жидкостью, плотность которой![]() кг/м
3 . В резервуаре над жидкостью создано
давлениер 0 = 0,2 МПа.
кг/м
3 . В резервуаре над жидкостью создано
давлениер 0 = 0,2 МПа.
|
|
Требуется : 1)
найти толщину стенки резервуара из
условия прочности в нижнем сечении,
если
2) построить эпюры окружных и меридиональных напряжений (вдоль меридиана). Решение. 1. В стенках
резервуара возникают меридиональные
|
При данном способе закрепления резервуара вес жидкости воспринимается основанием, поэтому меридиональные напряжения возникают только от действия внутреннего давления р 0 и равны
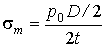 ,
,
а окружные напряжения возникают от давления газа и гидростатического давления р =р 0 + r g Н
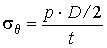 ,
,
![]() МПа
МПа
Используя четвертую теорию прочности
![]() ,
,
получим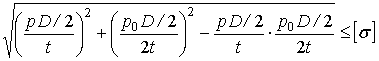 .
.
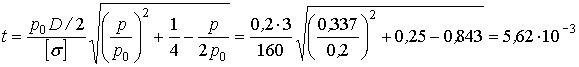 м.
м.
Округляя до большего целого значения, получим t = 6 мм.
2. Для построения эпюр меридиональных и окружных напряжений рассмотрим два участка: первый - часть резервуара выше уровня жидкости, второй - ниже уровня жидкости.
На первом участке
 МПа;
МПа;
![]() МПа.
МПа.
На втором участке меридиональные напряжения постоянны по всей высоте резервуара, а окружные напряжения линейно изменяются в зависимости от величины давления р =р 0 +r gz . В верхнем сечении (А ), на уровне поверхности жидкости, давлениер =р 0 = 0,2 МПа, в нижнем сечении резервуара (В ) -р =р 0 +r gH = 0,337 МПа(рис.16.2).
|
|
|
Литература: 1,§1.16; 2, §64,65.
![]()
Задача 19. РАСЧЕТ НА ВЫНОСЛИВОСТЬ
В опасном сечении вала диаметра d =
36 мм действуют крутящий моментМ к =
290 Нм и изгибающий моментМ и = 260
Нм. Вал из углеродистой стали (![]() в = 590 МПа,
в = 590 МПа,![]() Т = 280 МПа) не имеет резких переходов
диаметра, выточек, канавок, поверхность
его чисто обработана резцом.
Т = 280 МПа) не имеет резких переходов
диаметра, выточек, канавок, поверхность
его чисто обработана резцом.
Требуетсяопределить коэффициент запаса прочности в опасном сечении вала, приняв нормальные напряжения изгиба изменяющимися по симметричному циклу, а касательные напряжения кручения – по пульсирующему циклу (от нуля до максимального значения).
Коэффициенты концентрации напряжений и масштабные коэффициенты считать одинаковыми для нормальных и для касательных напряжений.
Решение.
1. Найдем максимальные нормальные напряжения изгиба и максимальные касательные напряжения кручения:
 МПа,
МПа,
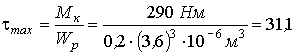 МПа,
МПа,
где W x ,W p – соответственно осевой и полярный моменты сопротивления.
2. По эмпирическим формулам находим
предел текучести при кручении
![]() Т
и пределы выносливости при кручении
и изгибе (при симметричном цикле)
Т
и пределы выносливости при кручении
и изгибе (при симметричном цикле)![]() -1
и
-1
и![]() -1
.
-1
.
Для углеродистых сталей
![]() ,
,![]() .
.
Примем
![]() МПа.
МПа.
![]() МПа;
МПа;
![]() МПа.
МПа.
3. Найдем действительный коэффициент концентрации по формуле
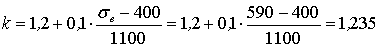 .
.
4. Найдем масштабный коэффициент
![]() .
.
5. Найдем коэффициенты запаса прочности по нормальным и касательным напряжениям.
При симметричном цикле среднее напряжение
и амплитуда цикла нормальных напряжений
соответственно равны
![]() ,
,![]() .
При пульсирующем цикле среднее напряжение
и амплитуда цикла касательных напряжений
соответственно равны
.
При пульсирующем цикле среднее напряжение
и амплитуда цикла касательных напряжений
соответственно равны
![]() МПа.
МПа.
Коэффициент запаса прочности по
усталостному разрушению при изгибе
![]() вычисляем
по формуле:
вычисляем
по формуле:
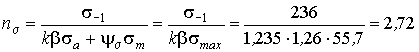 .
.
Для определения коэффициента запаса
прочности по усталостному разрушению
при кручении
![]() из
таблицы значений коэффициентов
из
таблицы значений коэффициентов![]() для
стали [1, табл.1.15] находим: при
для
стали [1, табл.1.15] находим: при![]() в
= 590 МПа = 59 кг/мм 2 ,
в
= 590 МПа = 59 кг/мм 2 ,![]() ,
приближенно принимаем
,
приближенно принимаем![]() .
.
Тогда
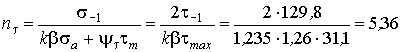 .
.
Коэффициент запаса прочности по текучести:
при изгибе
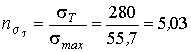 ;
;
при кручении
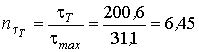 .
.
6. Найдем общие коэффициенты запаса прочности по усталостному разрушению n и по текучестиn Т :
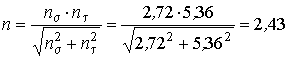 ,
,
 .
.
Литература: 1, гл.15; 2, гл.13.
![]()
Библиографический список
1. Дарков А.В., Кутуков Б.Н. Сопротивление материалов. 13 изд-е. М.: Высш. школа, 1979, 48 с.
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов. М., 1975, 654 с.
3. Сборник задач по сопротивлению материалов /Под ред. В.К.Качурина. М., 1972, 432 с.
4. Миролюбов И.Н., Енгалычев С.А., Сергиевский Н.Д. и др. Пособие к решению задач по сопротивлению материалов. М., 1962, 488 с.
5. Контрольные задания по сопротивлению материалов для студентов-заочников. Метод. указания /Сост.: С.Г.Сидорин, С.Г.Мухамбетжанов. КГТУ, Казань,. 1995, 40 с.
6. Сопротивление материалов. Опорный конспект лекций. Учеб. пособие /С.Г.Сидорин, Регентъ, 2003, 106 с.
![]()
|
|
Сопромат - заочно. Версия: 20 июня 2005 г. e-mail Сидорина С.Г. (sid_tlp@hotbox.ru) Кафедра теоретической механики и сопротивления материалов e-mail Нурутдинова А.И. (avianai82@mail.ru) Кафедра информатики и прикладной математики Казанский государственный технологический университет |


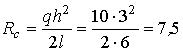 кН.
кН.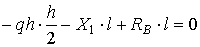
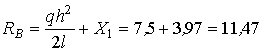 кН.
кН.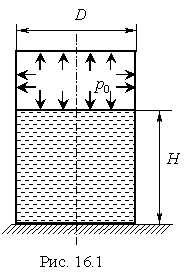

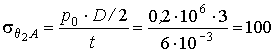 МПа,
МПа,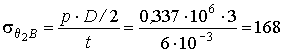 МПа.
МПа.