
- •Сопротивление материалов – заочно Для студентов заочной формы образования Казанского государственного технологического университета
- •Примеры решения задач Задача 1. Стержневая система
- •Задача 2. Статически неопределимая стержневая система
- •Задача з. Теория напряженного состояния
- •Задача 4. Кручение
- •Задача 5. Геометрические характеристики плоских сечений
- •Задача 6. Плоский изгиб
- •Задача 8. Внецентренное сжатие
- •Задача 9. Изгиб с кручением
Задача з. Теория напряженного состояния
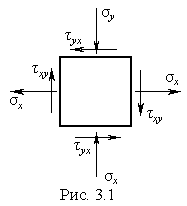
Элементарный параллелепипед, находящийся в произвольном месте стальной конструкции подвергается действию системы напряжений, лежащих в одной плоскости (рис.3.1).
|
|
Требуется найти: 1) главные напряжения и направление главных площадок; 2) максимальные касательные напряжения; 3)
главные деформации
4)
эквивалентное напряжение
5) относительное изменение объема; 6) удельную потенциальную энергию деформации. |
Исходные данные:
![]() х
= 90 МПа,
х
= 90 МПа,![]() у
= 80 M П a ,
у
= 80 M П a ,![]() х
y = 50 МПа.
х
y = 50 МПа.
Решение.
При выполнении этой задачи необходимо руководствоваться следующим правилом знаков для нормальных и касательных напряжений:нормальное напряжение положительно, если оно направлено по внешней нормали к плоскости сечения, то есть оно является растягивающим, а сжимающее - отрицательно. Касательное напряжение по боковой грани призмы положительно, если изображающий его вектор до совмещения с внешней нормалью следует повернуть против часовой стрелки.
Расставим знаки напряжений на рис. (3.1).
Получим:
![]() х
= -90 МПа,
х
= -90 МПа,![]() у
= -80 M П a ,
у
= -80 M П a ,![]() х
y = 50 МПа,
х
y = 50 МПа,![]() yх
=-50 МПа
yх
=-50 МПа
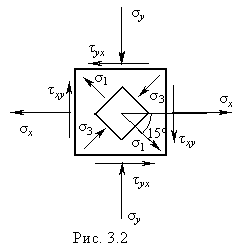
1. Найдем главные напряжения
|
|
Главные
напряжения обозначают
В задаче рассматривается плоское напряженное состояние, т.е. одно из трех главных напряжений равно нулю, поэтому из формулы (3.1)и правила(3.2)следует: |
|
|
|
|
Направление главных площадок относительно заданных площадок, определяется по формуле:
|
|
|
|
|
Отрицательный
угол |
2. Найдем максимальные касательные напряжения. Они равны наибольшей полуразности главных напряжений:
![]() МПа.
МПа.
3. Найдем главные деформации
![]() 1
,
1
,![]() 2
и
2
и![]() 3
из обобщенного закона Гука, приняв
коэффициент Пуассона равным V= 0,5:
3
из обобщенного закона Гука, приняв
коэффициент Пуассона равным V= 0,5:
|
|
|
|
|
|
4. Найдем эквивалентное напряжение
![]()
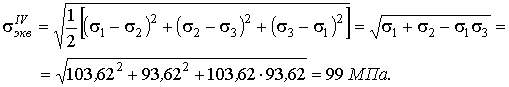
5. Найдем относительное изменение объема:
![]()
6. Найдем удельную потенциальную энергию деформации:
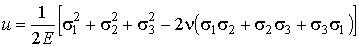
В данной задаче
![]() .
.
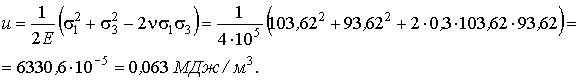
Литература: 1; §1.3-§9.3
![]()
Задача 4. Кручение
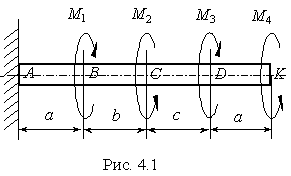
К стальному валу приложены скручивающие моменты: М 1 ,M 2 ,M 3 ,M 4(рис. 4.1).
|
|
Требуется 1) построить эпюру крутящих моментов; 2)
при заданном значении [
3) построить эпюру углов закручивания; 4) найти наибольший относительный угол закручивания. |
Исходные данные: М 1 =М 3 = 2 кНм,М 2 =М 4 = 1,6 кНм,а = b = с = 1,2
м, [![]() ]
= 80 МПа,[
]
= 80 МПа,[![]() ]=0,3.
]=0,3.
Решение.
1. Построить эпюру крутящих моментов.
Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются с помощью метода сечений. Крутящие моменты в произвольных поперечных сечениях бруса численно равны алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.
Рассекая последовательно участки вала, получим:
|
I участок ( КD ): |
|
|
II участок ( DC ): |
|
|
III участок ( СВ ): |
|
|
IV участок ( ВА ): |
|
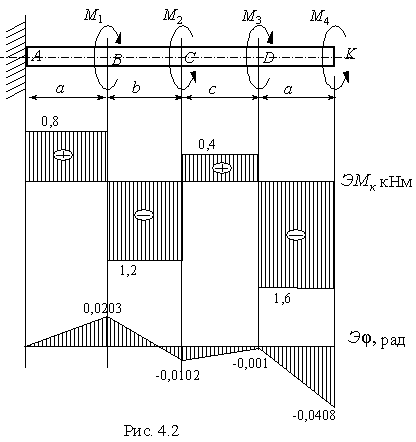
По значениям этих моментов строим эпюру М к в выбранном масштабе. Положительные значенияМ к откладываем вверх, отрицательные - вниз от нулевой линии эпюры (рис.4.2).
|
|
2. При заданном
значении [
где
Принимаем d = 50 мм = 0,05 м. |
3. Построим эпюру углов закручивания вала.
Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле
|
|
где GJ р - жесткость сечения вала при кручении. |
Модуль сдвига для стали
 Н/м
2
Н/м
2
|
|
J p - полярный момент инерции круглого вала |
Вычислим углы закручивания сечений В ,С ,D иК относительно закрепленного конца вала (сеченияА )
|
|
|
|
|
|
|
|
|
|
Строим эпюру углов закручивания (рис.4.2).
4. Найдем наибольший относительный угол закручивания
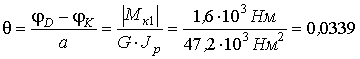 рад/м.
рад/м.
Литература: 1; §1.6-§4.6
![]()

 (3.1)
(3.1)

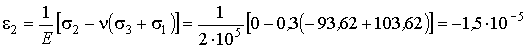
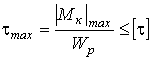
 мм.
мм.
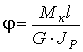
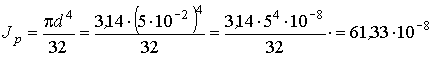 м
4 .
м
4 . 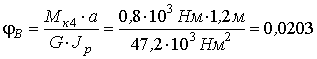 рад
рад рад,
рад,
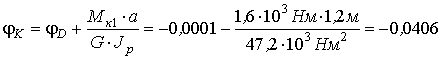 рад,
рад,
 рад.
рад.