1.5 Диаграмма удельных сил поезда

Диаграмма удельных сил поезда – это зависимость всех внешних удельных сил поезда от скорости его движения, сил, построенных в одной общей системе координат – рисунок 1.12.

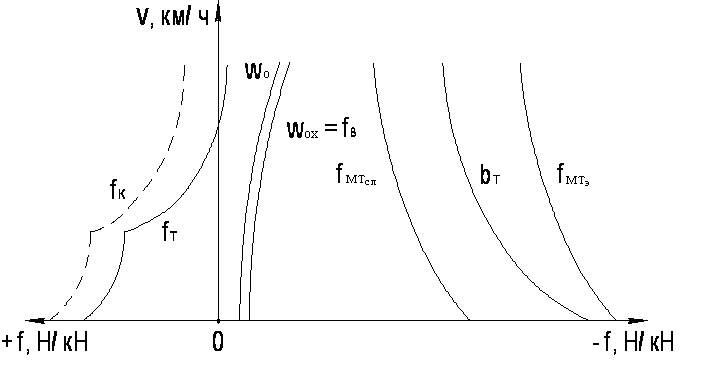
Рисунок 1.12 – Диаграмма удельных сил поезда

Теперь, имея зависимости каждой внешней удельной силы поезда от скорости его движения, можно построить диаграмму удельных равнодействующих сил поезда для всех трех возможных режимов движения поезда:

а) удельная равнодействующая сила поезда в режиме тяги:

f_т , (1.49)

б) удельная равнодействующая сила поезда в режиме выбега:

, (1.50)

в) удельная равнодействующая сила поезда в режиме механического торможения:

– экстренное торможение

f_мт.э = – b_т – , (1.51)

– служебное торможение

f_мт.сл = – 0,5·b_т – . (1.52)

Примечание. Так как дополнительное сопротивление движению поезда не является функцией скорости, а зависит от профиля пути, то на диаграмме удельных сил показывается только основное сопротивление движению поезда. Дополнительное сопротивление движению поезда учитывается в тяговых расчетах специальным способом.

1.6 Сила инерции поезда

Сила инерции поезда – это сила, появление которой связано с кинетической энергией, накопленной поездом при его движении.

В общем случае:

, (1.53)

где m, V – масса и скорость движения поезда;

J_кi, R_кi, ω_кi – момент инерции, радиус и угловая скорость i-й колесной пары;

J_яi, R_яi, ω_яi – момент инерции, радиус и угловая скорость i-го якоря

тягового двигателя.

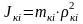, (1.54)

, (1.55)

, (1.56)

, (1.57)

где m_кi, m_яi, ρ_кi, ρ_яi – массы и радиусы инерции i-х колесных пар и якорей

двигателей;

µ – передаточное число зубчатой передачи локомотива.

Тогда из (1.53)…(1.57) получим:

, (1.58)

Обозначим

, (1.59)

где m_э – эквивалентная масса вращающихся частей поезда.

Теперь из (1.58) и (1.59):

, (1.60)

где ξ – переводный коэффициент, зависящий от принятой размерности фи-

зических величин. Например, при f, Н/кН; t, ч; S, км; V, км/ч:

ξ =127.

Обозначим

. (1.61)

Тогда из (1.59) и (1.60) получаем окончательно

, (1.62)

где – коэффициент инерции вращающихся частей поезда.

Например:

– для электровозов – ;

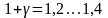– для груженых вагонов – ;

– для порожних вагонов – .

Величина коэффициента инерции для поезда, составленного из подвижного состава различного типа, определяется как средневзвешенное значение:

. (1.63)

В тяговых расчетах для пассажирских и грузовых поездов принимается следующее средневзвешенное значение коэффициента инерции:

. (1.64)