1.2 Сила тяги

1.2.1 Основной закон локомотивной тяги

Как известно, источником механической энергии для создания силы тяги на локомотиве являются электродвигатели (ТЭД), которые располагается на тележках локомотива и будучи подключенными к источнику электроэнергии создают на валах своих якорей вращающие моменты М_дв. Последние через зубчатые передачи (с коэффициентом передачи µ) образуют на колесных парах вращающие моменты М_к. Рассмотрим образование силы тяги на примере одной колесной пары – рисунок 1.2.

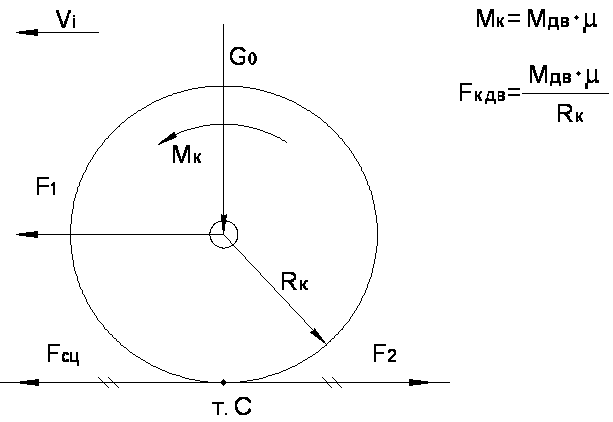
Рисунок 1.2 – Образования силы тяги

Здесь G₀ – сила тяжести локомотива, приходящаяся на одну ось колесной пары (или сила нажатия колеса на рельс), кН,

, (1.10)

где – число движущих осей локомотива.

Вращающий момент колесной пары может быть заменен парой сил F1 и F2. При этом сила F1 приложена к оси колесной пары, а сила F2 – к рельсу в точке «С» касания колеса и рельса. Очевидно

F1 = F2 = . (1.11)

В соответствии с 3-м законом Ньютона в точке «С» возникает реактивная сила F_сц, которая приложена уже к колесу, равна по величине силе F2, но противоположна ей по направлению. Таким образом, силы F2 и F_сц взаимно уравновешивают друг друга, т.е. нижняя точка колеса как бы фиксируется на рельсе, и тогда под действием силы F1 ось колесной пары перемещается влево: начинается перекатывание колеса по рельсу, т.е. поступательное движение локомотива с составом с какой-то скоростью v_i. При этом сила тяги локомотива F_к равна:

. (1.12)

Силу F_сц называют силой сцепления (колеса с рельсом). В результате образования именно этой силы создается мгновенный центр вращения колеса в точке «С» и происходит преобразование вращающего момента колесной пары в силу тяги . При нормальном движении всегда:

. (1.13)

Условием же нормального движения (без боксования) является следующее условие:

. (1.14)

где – максимально возможная (потенциальная) сила сцепления коле-

са и рельса,

, (1.15)

– коэффициент сцепления колеса и рельса.

Из (1.14) и (1.15) следует:

, (1.16)

Выражение (1.16) – это и есть основной закон локомотивной тяги: для получения нормального движения (без боксования) сила тяги двигателя должна быть меньше или, в крайнем случае, равна максимально возможной (потенциальной) силы сцепления колеса с рельсом!

1.2.2 Коэффициент сцепления

Физическая природа коэффициента сцепления та же, что и коэффициента трения двух поверхностей, но имеющая свою специфику.

Под действием вертикальной нагрузки G₀ от колеса на рельс происходит упругая деформация металла, в результате которой образуется небольшая контактная площадка, называемая контурной. Поверхности колес и рельсов имеют шероховатости, поэтому давление воспринимается отдельными выступами так, что площадь истинного контакта составляет около 10 % от контурной площадки. При этом под действием вертикальной нагрузки происходит взаимное внедрение неровностей колеса и рельса, возникает зацепление микроповерхностей – чисто механическое противодействие смещению поверхностей колеса и рельса. Кроме того, в результате сжатия микровыступов происходит еще и пластическая деформация, при которой связь соприкасающихся поверхностей колеса и рельса обусловлена еще и их молекулярным взаимодействием.

Итак, явление сцепление колеса с рельсом имеет двойственную механико-молекулярную физическую природу. Кроме того, имеет место и, так называемые, упругие скольжения колеса и рельса, направленные в противоположные стороны, что приводит к появлению трения скольжения.

Коэффициент сцепления определяется опытным путем как отношение наибольшей реализуемой в эксплуатации силы тяги локомотива к силе тяжести локомотива:

, (1.17)

Такой коэффициент сцепления называется расчетным. Эксперименты показали, что он ( ) зависит от скорости движения поезда и в общем случае может быть определен по следующей эмпирической формуле:

, (1.18)

где значения коэффициентов a, b, c, d, e определяются серией локомотива и приводятся в ПТР [1].

Зависимость приведена на рисунке 1.3, где отдельными точками показаны значения коэффициента сцепления, полученные экспериментальным путем.

Рисунок 1.3 – Зависимость коэффициента сцепления от скорости

движения

1.2.3 Тяговые характеристики локомотива

Тяговая характеристика локомотива – это зависимость силы тяги F_к локомотива от скорости v движения поезда F_к(v) при постоянном напряжении на ТЭД.

Очевидно, тяговая характеристика локомотива определяется тяговой характеристикой электродвигателя, в качестве которого в настоящее время на всех локомотивах применяется практически один тип электродвигателя – ТЭД постоянного тока последовательного возбуждения.

, (1.19)

, (1.20)

, (1.21)

, (1.22)

. (1.23)

Рисунок 1.4 – Принципиальная электрическая схема ТЭД постоянного тока

последовательного возбуждения

На тяговую характеристику накладываются ограничения – рисунок 1.5:

а) по сцеплению – по (1.15);

б) по конструкционной скорости V_к локомотива.

Рисунок 1.5 – Характеристики локомотива с ТЭД последовательного

возбуждения