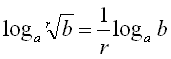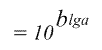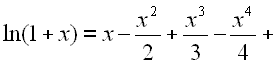Степени и корни (свойства)

1.

Любое число в нулевой степени равно 1.

2. 

При умножении степеней с одинаковыми основаниями, основание остается прежним, а показатели складываются.

3. 

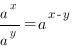
При делении степеней с одинаковыми основаниями, основание остается прежним, а показатели вычитаются.

4.  

При возведении в степень произведения, в эту степень возводится каждый множитель.

5.  

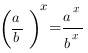
При возведении в степень дроби в эту степень возводится числитель дроби и знаменатель.

6. 

При возведении степени в степень показатели перемножаются.

7. 

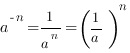
При возведении в отрицательную степень, основание степени «переворачивается», и знак  показателя степени меняется на противоположный.

Корни.

:

Арифметическим корнем n-ой степени из неотрицательного числа  называется неотрицательное число, n-я степень которого равна  :

Внимание! Степень корня – это натуральное число, большее 1.

, 

,  Свойства корня n-ой степени:

1. 

2. 

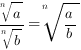
3. 

4. 

5.

Частные случаи:

1. Если показатель корня целое нечетное число ( ), то подкоренное выражение может быть отрицательным.

В  случае нечетного показателя уравнение   при любом действительном значении   и целом    ВСЕГДА имеет единственный корень:

,

Для корня нечетной степени справедливо тождество:

,

2. Если показатель корня целое четное число ( ), то подкоренное выражение  не может быть отрицательным.

В  случае четного показателя уравнение   имеет

при   единственный корнь 

и, если  , два корня:

   и  

Для корня четной степени справедливо тождество:

Внимание! Для корня четной степени справедливы равенства:

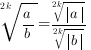
Показательная функция, ее свойства и графики

Функция вида  называется показательной функцией.

Замечание. Исключение из числа значений основания a чисел 0; 1 и отрицательных значений a объясняется следующими обстоятельствами:

a = 0	Выражения вида 0x определено при x > 0 и в этом случае тождественно равно нулю.
a = 1	Выражение 1x определено при всех x, имеет постоянное значение (тождественно единице).
a < 0	Возможно возведение в целую степень или в рациональную степень с нечётным знаменателем.

Само аналитическое выражение a^x в указанных случаях сохраняет смысл и может встречаться в решении задач. Например, для выражения x^y точка x = 1; y = 1 входит в область допустимых значений.

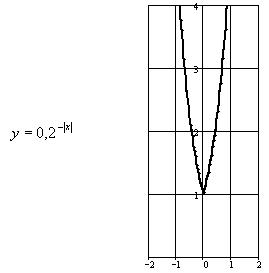
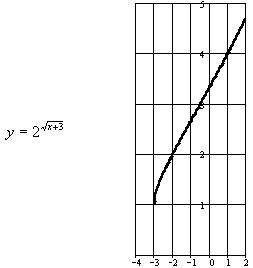
Построить графики функци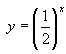й:   и  .

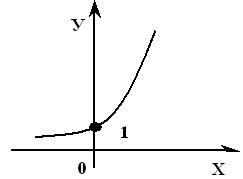
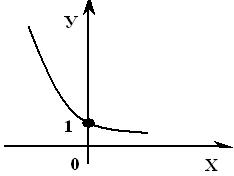
График показательной функции
y = ax , a > 1	y = ax , 0< a < 1

Свойства показательной функции

Свойства показательной функции	y = ax , a > 1	y = ax , 0< a < 1
Область определения функции
2. Область значений функции
3.Промежутки сравнения с единицей	при x > 0, ax > 1	при x > 0, 0< ax < 1
	при x < 0, 0< ax < 1	при x < 0, ax > 1
4. Чётность, нечётность.	Функция не является ни чётной, ни нечётной (функция общего вида).
5.Монотонность.	монотонно возрастает на R	монотонно убывает на R
6. Экстремумы.	Показательная функция экстремумов не имеет.
7.Асимптота	Ось Ox является горизонтальной асимптотой.
8. При любых действительных значениях xи y;

Когда заполняется таблица, то параллельно с заполнением решаются задания.

Задание № 1. (Для нахождения области определения функции).

Какие значения аргумента  являются допустимыми для функций:

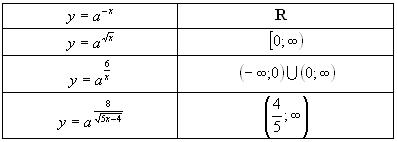
Задание № 2. (Для нахождения области значений функции).

На рисунке изображен график функции. Укажите область определения и область значений функции:

Задание № 3. (Для указания промежутков сравнения с единицей).

Каждую из следующих степеней сравните с единицей:

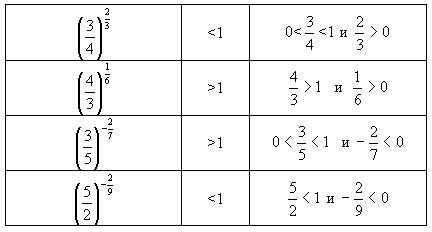
Задание № 4. (Для исследования функции на монотонность).

Сравнить по величине действительные числа m и n если:

Задание № 5. (Для исследования функции на монотонность).

Сделайте заключение относительно основания a, если:

В одной координатной плоскости построены графики функций:

y(x) = 10^x; f(x) = 6^x; z(x) - 4^x

Как располагаются графики показательных функций относительно друг друга при x > 0, x = 0, x < 0?

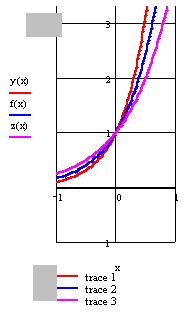
Вывод:

 

при x < 0	чем больше значение основания степени, тем ближе к оси Oxрасполагается график показательной функции;
при x = 0	графики показательных функций пересекаются в одной точке (0;1);
при x > 0	чем больше значение основания степени, тем дальше от осиOxрасполагается график показательной функции.

В одной координатной плоскости построены графики функций:

y(x) = (0,1)^x; f(x) = (0,5)^x; z(x) = (0,8)^x.

Как располагаются графики показательных функций относительно друг друга при x > 0, x = 0, x < 0?

Вывод:

при x < 0	чем меньше значение основания степени, тем дальше от оси Oxрасполагается график показательной функции;
при x = 0	графики показательных функций пересекаются в одной точке (0;1);
при x > 0	чем меньше значение основания степени, тем ближе к осиOxрасполагается график показательной функции.

Число   одна из важнейших постоянных в математике. По определению, оно равно пределу последовательности   при неограниченном возрастании n. Обозначение e ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака этого числа в десятичной записи, а само число назвали в честь Непера «неперовым числом». Число e играет особую роль в математическом анализе. Показательная функция с основанием e, называется экспонентой и обозначается y = ex. Первые знаки числа e запомнить несложно: два, запятая, семь, год рождения Льва Толстого - два раза, сорок пять, девяносто, сорок пять.

Логарифмические функции(свойства и график)

«Свойства и график логарифмической функции»

Функция у = lоgа х, где а — заданное число, а > 1, называется логарифмической функцией.0, а

Свойства логарифмической функции у = lоgа х

1. Область определения функции — множество всех положительных чисел (х > 0).

2. Область значений функции — множество R всех действительных чисел.

3. Монотонность функции:

если а > 1, то функция является возрастающей;

если 0 < а < 1, то функция является убывающей. Промежутки постоянного знака:

1	Значения аргумента	a > 1	0 < а < 1
2	0< х < 1	у< 0	у > 0
3	Х > 1	у> 0	у < 0

.

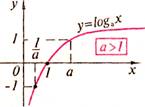
График логарифмической функции у =lоg а х расположен правее оси ОУ и проходит через точку (1; 0).

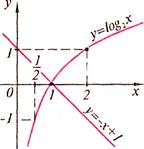
Основные свойства логарифмов

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называютсяосновными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log_a x и log_a y. Тогда их можно складывать и вычитать, причем:

1. log_a x + log_a y = log_a (x · y);

2. log_a x − log_a y = log_a (x : y).

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь —одинаковые основания. Если основания разные, эти правила не работают!

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Теорема

Пусть дан логарифм log_a x. Тогда для любого числа c такого,что c > 0 и c ≠ 1, верно равенство:

В частности, если положить c = x, получим:

Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача

Найдите значение выражения: log₅ 16 · log₂ 25.

Решение

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log₅ 16 = log₅ 2⁴ = 4log₅ 2;log₂ 25 = log₂ 5² = 2log₂ 5;

А теперь «перевернем» второй логарифм:

Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Ответ

8

Натуральный и десятичный логарифм

Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).

 

Основное логарифмическое тождество
Покажем как можно любую функцию вида abсделать экспоненциальной. Поскольку функция вида ех называется экспоненциальной, то
Любая функция вида a bможет быть представлена в виде степени десяти

 

Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045… )  ln(e)=1;  ln(1)=0

При		логарифм числа (1+х) разлагается в ряд:
Например,

 

Ряд сходится, но медленно и значение x ограничено весьма узким диапазоном. Но ряд:

сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа z .

Производная натурального логарифма:

 

Десятичный логарифм lg (логарифм по основанию "10").  lg(10)=1;  lg(1)=0

Если: а = b · 10 n То: lg a = lg b + n Кроме того: 10 x = 10 { x } · 10 [ x ] , где { x } — дробная часть x , а [ x ] — целая часть x .

определение тригонометрических функций в прямоугольном треугольнике

Чтобы определить тригонометрические функции произвольного угла α, возьмём произвольный прямоугольный треугольник, содержащий угол α.

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π. Это означает, что углы между катетами и гипотенузой лежат между 0 и  Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Си́нус угла — отношение противолежащего катета к гипотенузе:   Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны.

Ко́синус угла — отношение прилежащего катета к гипотенузе:   Так как   синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Та́нгенс угла — отношение противолежащего катета к прилежащему: 

Кота́нгенс угла — отношение прилежащего катета к противолежащему:   Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Из определений тригонометрических функций следует:

и симметрично:

Определение тригонометрических функций

Ключевые слова: синус, косинус, тангенс, котангенс, радиан, угол

Рассмотрим на координатной плоскости окружность радиуса R = 1 с центром O в начале координат. Координатные оси делят окружность на четыре дуги, которые называют четвертями.

Рассмотрим произвольный угол  . Точка  M(x;y) лежит на единичной окружности, считаем, что точка  M результат поворота точки A(1;0) на угол  . На оси OX находятся значения cosугла поворота, а на оси OY, соответственно, находятся значения  sin углов поворота. На дополнительных осях ctg и tg  параллельных осям OX и OY, соответственно, находятся значения  ctg и tg  угла поворота. Тригонометрические функции (функции угла) определяются следующими равенствами: синус: sin =y, т.е. ордината точки M; косинус: cos =x, т.е. абсцисса точки M; тангенс: tg =xy, т. е. отношение ординаты к абсциссе точки M; котангенс: ctg =yx, т. е. отношение абсциссы к ординате точки M. Замечание.  Значение tg  угла поворота не существует для углов 2 + n n Z .Значение ctg  угла поворота не существует для углов  n n Z .

Схемы определения тригонометрических функций (функций угла):

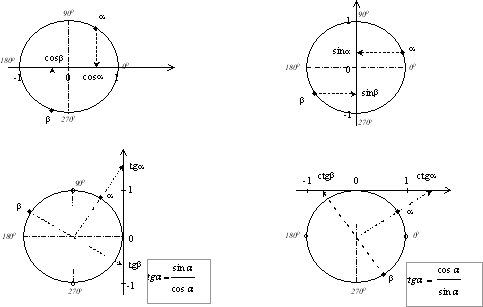
Тригонометрические функции(свойства и графики)

Функция синус

Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R.  График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2π: sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R. sin x = 0 при x = π·k, k ∈ Z. sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z. sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z. Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках: Наибольшее значение функции sin x = 1 в точках: Наименьшее значение функции sin x = −1 в точках:

Функция косинус

Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R.  График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом 2π: cos(x+2π·k) = cos x, где k ∈ Z для всех х ∈ R. cos x = 0 при cos x > 0 для всех cos x < 0 для всех Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках: Наибольшее значение функции sin x = 1 в точках: Наименьшее значение функции sin x = −1 в точках:

Функция тангенс

Область определения функции — множество всех действительных чисел, кроме Множество значений функции — вся числовая прямая, т.е. тангенс — функция неограниченная. Функция нечетная: tg(−x)=−tg x для всех х из области определения.  График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения. 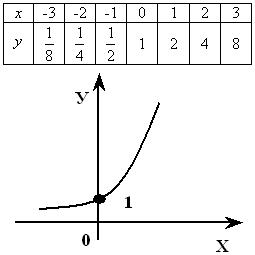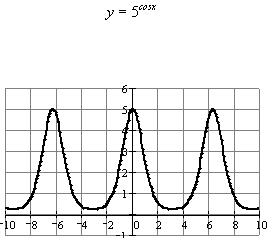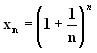tg x = 0 при tg x > 0 для всех tg x < 0 для всех Функция возрастает на промежутках: