Где: pv – текущая или сегодняшняя стоимость;

FV – расчетная будущая стоимость;

n – количество периодов;

i – ставка дохода.

Сомножитель (1 + i)ⁿ в дальнейшем будем называть фактором суммы единицы по сложному проценту, а его значение определять по первой колонке стандартной таблицы шести функций сложного процента. В таблице приведены данные для годового и ежемесячного начисления дохода.

Пример.

Стоимость земли, купленной за 20000 рублей, повышается в среднем на 15% в год. Определить, какова будет ее стоимость через 5 лет без учета налогов, страховых сборов и торговых издержек.

Решение по таблице:

FV = 20000 × кол.1 = 20000 × 2,01136 = 40227,1437 руб.

15%

5 n

Эту задачу можно решить с помощью финансового калькулятора модели «CASIO» (или любой другой модификации). Чтобы с помощью калькулятора определить будущую стоимость FV, необходимо:

1. осуществить «вход» в программу «6 функций» сложного процента последовательным нажатием следующих клавиш:

mode

1

mode

6

shift

АС

На дисплее должен быть установлен знак «ОК». Эта же процедура выполняет роль «чистки» калькулятора от всех предыдущих показателей и осуществляется перед каждым новым вычислением;

2. осуществить ввод всей исходной информации строго последовательно: вначале числовую характеристику переменной, затем ее обозначения. Порядок ввода самих переменных значения не имеет. При этом следует иметь в виду: если вводятся в качестве исходной информации две стоимостные характеристики, например, PV и FV, то одна из них должна вводиться со знаком +/-;

3. результаты расчета получаются путем последовательного нажатия клавиш «cоmp» и того параметра, который следует определить.

Ниже показано, какие клавиши финансового калькулятора «CASIO» необходимо использовать для определения будущей стоимости земельного участка.

mode

1

mode

6

shift

АС

20000 PV

15. i

5. n

cоmp FV

Результат 40227,14375 (на дисплее).

Пример.

Господин Иванов взял кредит в банке в сумме 10000 рублей под 15% годовых на 3 года с условием, что и основная сумма долга, и проценты будут выплачены разовым платежом в конце срока кредитования. Какова будет сумма выплат:

1. при годовом начислении процента;

2. ежемесячном начислении процента.

Решение.

1. При условии годового начисления процента:

• по таблице шести функций сложного процента: FV = 10000 × кол.1 =

=10000 × 1,520875 = 15208,75 руб.; 15%

3n

• на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

10000 PV

15 i

3 n

cоmp FV

Результат 15208,75 руб., (на дисплее).

2. При условии ежемесячного начисления процентов:

• по таблице (ежемесячного начисления процентов): FV = 10000 × кол.1 =

15 i

3 n

=10000 × 1,563944 = 15639,44 (руб.)

– на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

10000 PV

15 shift i

3 shift n

cоmp FV

Результат 15639,44 руб., (на дисплее).

К

shift

лавиша позволяет производить вычисления только при ежемесячном начислении процента.

Вторая функция сложного процента – текущая стоимость реверсии.

Функция показывает сегодняшнюю или текущую стоимость одной денежной единицы, которая должна быть получена единовременно в будущем. Данная функция является обратной по отношению к первой функции – накопленной сумме денежной единицы. Это есть функция дисконтирования (discount – уменьшать).

Графически эта функция представлена на рис. 2.

FV

PV

i

?

n

Рис. 2. Текущая стоимость единицы или реверсии

Текущая стоимость реверсии определяется по формуле:

PV = FV x 1/(1 + i)ⁿ; PV = FV × кол. 4 (2)

где: 1/(1 + i)ⁿ – фактор текущей стоимости единицы или реверсии, определяется по 4 колонке таблицы шести функций сложного процента (дисконтный множитель);

i – ставка дисконтирования.

Пример.

Определить, какая цена в денежном выражении может быть оплачена сегодня за объект недвижимости, если через четыре года, по прогнозам его можно будет продать за 400000 рублей. Доходность аналогичных по уровню риска инвестиций составляет 12%.

Решение:

• по таблице шести функций сложного процента:

PV = 400000 × кол. 4 = 400000 × 0,635518 = 254207,2;

12 i

4 n

– на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

400000 FV

12 i

4 n

cоmp FV

Результат 254207,2 руб. (на дисплее).

Пример.

Семья планирует путешествие за границу через 4 года. Стоимость поездки ориентировочно составит 5000 долларов. Определить, какую сумму следует положить на депозит под 14% годовых сегодня, чтобы накопить нужную сумму.

Решение:

• по таблице шести функций сложного процента:

PV = 5000 × кол. 4 = 5000 × 0,592080 = 2960,4 (доллара)

14 i

4 n

- на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

5000 FV

14 i

4 n

cоmp FV

Результат 2960,4 долл.(на дисплее).

Пример.

На счет под 13% годовых положили 10000 у.е. Определить срок, когда на счете будет аккумулирована сумма в 12769 у.е.

Д ано:

PV = 10000 FV = PV (1 + i)ⁿ

I = 13%

F V = 12769

n - ? По таблице сложных процентов находим значение n=2.

На финансовом калькуляторе:

mode

1

mode

6

shift

АС

10000 +/- PV

13 i

12769 FV

cоmp n

Если вводятся две денежные единицы, то одна из них обязательно вводится со знаком +/–.

Третья функция сложного процента – текущая стоимость аннуитета.

Обычный аннуитет определяется как серия равновеликих платежей, первый из которых осуществляется через один период, начиная с настоящего момента. Он также определяется как серия поступлений. Например, право получать 100 рублей в конце каждого года в течение следующих 4 лет создает обычный аннуитет. Аналогично обязательство ежемесячно выплачивать 100 рублей в течение следующих 30 месяцев является обычным аннуитетом.

Текущая стоимость аннуитета показана графически на рис. 3.

?

PV

i

1 2 3 … n

Рис. 3. Текущая стоимость аннуитета

Текущая стоимость аннуитета при заданной ставке дисконта может быть рассчитана путем оценки каждого платежа (поступления) в отдельности. При этом сумма каждого платежа умножается на соответствующий фактор текущей стоимости единицы.

Например, право получения 2000 рублей в виде арендной платы в конце каждого года на протяжении 3 лет может быть оценено при 12% ставке дисконта, если каждое поступление рассматривать как текущую стоимость реверсии. Тогда, используя вторую функцию сложного процента, можно определить текущую стоимость серии равновеликих и равноудаленных поступлений.

Расчет представлен графически на рис. 4.

1423,56

1594,38

4803,64

1785,7

2000

2000

2000

руб.

Рис. 4. Текущая стоимость арендных платежей

Предварительно рассчитанные таблицы. Широкое и интенсивное использование фактора текущей стоимости аннуитета привело к построению соответствующих таблиц. Они показывают факторы с учетом того, что каждый платеж за период равен 1 доллару. В таблицах шести функций сложного процента данный фактор приведен в 5 колонке.

Текущая стоимость обычного аннуитета рассчитывается по формуле:

1

P V = PMT 1 – (1 + i)ⁿ ; PV = PMT × кол. 5. (3)

i

Авансовый аннуитет. Некоторые аннуитеты структурированы таким образом, что первое поступление (платеж) в потоке доходов происходит немедленно, последующие же платежи производятся через равные интервалы. Такие аннуитеты называются авансовыми.

Для того, чтобы оценить подобный аннуитет, рассмотрим первый платеж, осуществляемый на полную сумму. Он производится немедленно, поэтому дисконтировать его не следует. Последующие поступления дисконтируются. Поскольку второе поступление произойдет через один временной интервал от настоящего момента, его следует оценивать с использованием фактора текущей стоимости реверсии для первого интервала. Чтобы превратить фактор обычного аннуитета в фактор авансового аннуитета, необходимо взять фактор обычного аннуитета для потока доходов, укороченного на один период, и добавить к нему единицу. При добавлении единицы как раз и учитывается первое поступление. При сокращении потока на один период во внимание принимается текущая стоимость остальных платежей, т.е. последний платеж не учитывается.

Графически расчет серии авансовых аннуитетов представлен на рис.5.

Руб.

PV

i

1

1

1

1

1

…

PMT n

Рис. 5. Текущая стоимость авансового аннуитета

Формула расчета текущей стоимости авансового аннуитета:

1

P V = PMT 1 – (1 + i)^n-1 ; PV = PMT × кол. 5 + 1 . (4)

i +1 n – 1

i

Финансовый калькулятор «CASIO» для расчета авансового аннуитета предусматривает клавишу «BGN».

Пример.

Инвестор рассматривает перспективу покупки здания, которое будет приносить доход в течение 8 лет по 17000 руб. чистой арендной платы в конце каждого года. В конце 8 года инвестор планирует продажу объекта за 140000 руб., средняя годовая ставка дохода – 14%.

Определить максимально возможную цену, за которую можно купить этот объект сегодня.

Условия задачи в виде графика представлены на рис.6.

PV₂

140000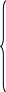

i = 14% FV

PV₁

PV₀ PMT = 17000

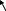
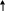
n = 8 лет

Рис. 6. Текущая стоимость арендных платежей и реверсии (перепродажи)

Решение:

• по таблице шести функций сложного процента:

кол. 5

PV₁ = PMT 14i = 17000 × 4,63886 = 78860,68 (руб.) – текущая

8 n стоимость серии арендых платежей;

• на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

17000 PМТ

14 i

8 n

cоmp PV

Результат: 49078,27 у.е.

кол. 4

PV₂ = FV 14 i = 140000 × 0,350559 = 49078,27 (руб.) – текущая

8 n стоимость реверсии.

Расчет PV₂ на калькуляторе:

mode

1

mode

6

shift

АС

140000 FV

14 i

8 n

cоmp PV

Результат: 49078,27 (руб.)

Общее значение текущей стоимости аннуитета и реверсии:

PV₀ = 78860,68 + 49078,27 = 127938,95 (руб.)

Эту же задачу можно решить с помощью финансового калькулятора в режиме шести функций в одно действие:

17000 PМТ

140000 FV

14 i

8 n

cоmp PV

Результат: 127938,95 (руб.).

При данных условиях стоимость объекта может составить 127939 (руб.)

Рассмотрим этот же пример, но при условии, что арендные платежи будут поступать не в конце, а в начале каждого года.

Графически условия задачи могут быть представлены, как показано на рис.7.

PV₂

140000

FV

PV₁

PV₀ PMT = 1700

1 2 3 4 5 6 7 8 n

Рис. 7. Текущая стоимость арендных платежей и реверсии (перепродажи)

Решение.

1. 1. Определим текущую стоимость авансового аннуитета:

• по таблице шести функций сложного процента:

кол. 5

PV₁ = 17000 i 14 + 1 = 17000 (4,28830 + 1) = 89901,1(руб.) .

(8-1) n

• то же на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

17000 PМТ

BGN

14 i

8 n

cоmp PV

Результат: 89901,1 (руб.)

2. Текущая стоимость реверсии по результатам предыдущего решения составляет 49078,27 (руб.).

3. Общая текущая стоимость потока доходов составит:

89901,1 + 49078,27 = 138979,37 (руб.).

Эту же задачу можно решить с помощью финансового калькулятора в режиме шести функций в одно действие:

mode

1

mode

6

shift

АС

17000 PМТ

BGN

14 i

8. n 140000 FV

cоmp PV

Результат: 138979,4 (руб.).

Таким образом, мы видим, что один и тот же объект собственности, обеспечивающий получение авансовых аннуитетных платежей, имеет более высокую стоимость, чем при обычном аннуитентном потоке. Поэтому арендодатель всегда стремится заключить договор аренды на условиях авансовых платежей.

В реальной практике арендные, или ипотечные, платежи могут периодически либо увеличиваться, либо уменьшаться. В случае, когда платеж должен возрастать, возникает повышающаяся аренда. Такой подход арендодатели часто используют для нивелирования инфляционных рисков. Снижение кредитных платежей может использоваться для учета износа собственности по мере ее устаревания. Кроме того, учет факторов инфляции и рисков получения (неполучения) запланированных доходов может быть осуществлен путем изменения ставки дисконта. При этом чем дальше период получения доходов и, соответственно, выше риск, тем выше будет ставка дисконта.

Пример.

Договор аренды офисного помещения заключен на 4 года. Арендные платежи должны осуществляться в конце каждого года, причем первые два года – в размере 10000 руб., следующие два года – по 15000 руб. При номинальной ставке 10% определить, какая сумма может быть уплачена сразу после заключения договора аренды в виде разового единовременного платежа.

Решение.

Графически задача представлена на рис. 8.

i = 10%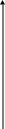

PV

?

15000

15000

10000

10000

1 2 3 4

Рис. 8. Текущая стоимость увеличивающегося потока платежей

Данную задачу можно решить несколькими способами:

1. Оценить текущую стоимость потока выплат как сумму отдельных реверсий путем последовательного дисконтирования каждого платежа и их последующего суммирования (задача потребует выполнения 5 действий);

2. Можно оценить 4-летний поток ежегодного дохода в 15000 руб., затем вычесть текущую стоимость потока ежегодного дохода в 5000 руб., прибавленного к первым двум выплатам. Решение на финансовом калькуляторе «CASIO»:

mode

1

mode

6

shift

АС

15000 PМТ

10. i

4 n

cоmp PV₁

Результат: 47547,98 руб. – текущая стоимость 4-летнего аннуитетного потока в 15000 рублей.

mode

1

mode

6

shift

АС

5000 PМТ

10 i

2 n

cоmp PV₂

Результат: 8677,68 руб. – текущая стоимость двухлетнего аннуитетного потока в 5000 рублей.

Единовременная стоимость договора аренды составляет:

PV₀ = PV₁ – PV₂ = 47547,98 – 8677,68 = 38870,3 руб.

Г

i = 10%

PV

рафически решение задачи можно представить, как показано на рис.9.

PV₂

15000

15000

PV₁

PV₀

5000

5000

10000

1000

РМТ n

Рис. 9. Текущая стоимость арендных платежей

3. Можно оценить 4-летний поток ежегодных арендных выплат в 10000 рублей, затем добавить текущую стоимость ежегодных выплат в 5000 рублей, получаемых в течение последних 2-х лет.

PV₁ – текущая стоимость аннуитетного потока арендных выплат в 10000 рублей

кол. 5

PV₁ = 10000 10 i = 10000 × 3,16987 = 31698,7 руб.

4 n

PV₂ – текущая стоимость ежегодных выплат в 5000 руб., получаемых в течение последних 2-х лет.

Графически решение может быть представлено в следующем виде:

(PV)

i = 10 FV i = 10

PV₂ 5000 5000

n = 2 3 4 n

Рис. 10. Текущая стоимость аннуитетного потока в 5000 руб., получаемого в 3 и 4 годы

PV₂ = 5000 × кол. 5 × кол. 4 = 5000 × 1,73554 × 0,826446 = 7171,65 руб.

10 i 10 i

2 n 2 n

Единовременная стоимость договора аренды составляет:

PV₂ = 7171,65 + 31698,7 = 38870,3 руб.

Четвертая функция сложного процента – накопление единицы за период.

Функция позволяет определить сумму, которая будет накоплена за определенный период, если регулярно откладывать по 1 денежной единице. Сущность данной функции можно рассмотреть на примере: вкладчик депонирует 1 рубль в конце каждого года в течение 4 лет при ставке 10% и ежегодном накоплении. Рубль, депонированный в конце первого года, будет приносить процент в течение последующих трех лет; рубль, депонированный по окончании второго года, в течение двух; в конце третьего года – в течение одного года; наконец, рубль, депонированный в конце четвертого года, вообще не принесет процента.

Широкое применение накопления единицы за период привело к составлению соответствующих таблиц, показывающих данные факторы в расчете на 1 денежную единицу периодического депозита. В таблице шести функций сложного процента данный фактор приведен в колонке 2. Факторы рассчитаны при депонировании сумм в конце каждого периода.

Графически функция накопления единицы за период представлена на рис. 11.

Р уб.

Про- цент

Доход

4

Возврат депонированной суммы, i

3

2

1

n

РМТ

1 2 3 … n

Рис.11. Накопление единицы за период

Формула определения будущей стоимости обычного аннуитетного потока поступлений (выплат):

(1 + i)ⁿ – 1

F V = PMT FV = PMT × кол. 2 (5)

i i

n

Предположим, что студент по окончании каждого лета способен вносить 100 долл. на счет, приносящий 10% годовых. К концу четвертого лета он получит 4641 долл., которые он может направить на первый взнос за обучение на 5 курсе. Процесс накопления описан графически на рис. 11. В табл. 5 показана структура накопления.

Таблица 5