Постоянный электрический ток Трудности классической теории

Температурная зависимость сопротивления. Из формулы удельной проводимости следует, что сопротивление металлов, т. е. величина, обратно пропорциональ­ная , должна возрастать пропорционально (в (103.2) п и l от температуры не зависят, а u~ ). Этот вывод электронной теории противоречит опытным данным, согласно которым R~T.

Оценка средней длины свободного пробега электронов в металлах. Чтобы по фор­муле получить , совпадающие с опытными значениями, надо принимать l значительно больше истинных, иными словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Со­гласно закону Дюлонга и Пти (см. § 73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна ³/₂R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классичес­кой электронной теорией.

Объяснить затруднения элементарной классической теории электропроводности метал­лов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени.

Электромагнетизм. Циркуляция вектора в магнитного поля по замкнутому контуру

Циркуляцией вектора В по заданно­му замкнутому контуру называется интеграл

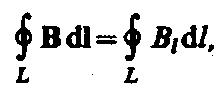
где dl — вектор элементарной длины контура, направленной вдоль обхода контура,

B_l=Bcos — составляющая вектора В в направлении касательной к контуру

(с учетом выбранного направления обхода),  — угол между векторами В и dl.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В):

циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной ₀ на алгебраическую сумму токов, охватываемых этим кон­туром:

(118.1)

где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным.

Выражение (118.1) справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи.

Движение заряженных частиц (в однородном) магнитном поле

Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол  между векторами v и В равен 0 или . Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центро­стремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

Если скорость v заряженной частицы направлена под углом  к вектору В, то ее движение можно представить в виде суперпозиции:

1. равномерного прямолиней­ного движения вдоль поля со скоростью v_||=vcos;

2. равномерного движения со скоростью v_=vsin по окружности в плоскости, перпендикулярной полю.

В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии