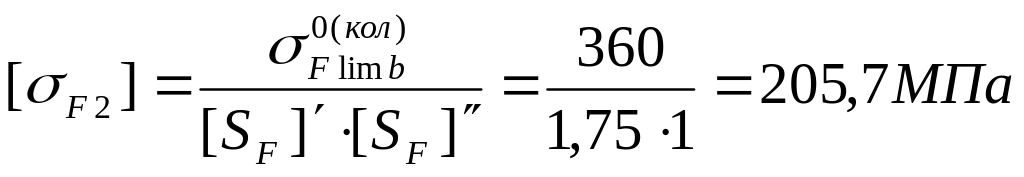4.3.10 Определение внешнего диаметра шестерни и колеса по вершине зубьев

Расчет произведем по ГОСТ 19624-74 (таблица 3.11., источник №1, стр.50).

Внешний диаметр шестерни и колеса по вершине зубьев:

Для шестерни: d_ae1 = d_e1+ 2h_aecos₁ =72+2x2,8xcos17,61= 76,5 мм

Для колеса: d_ae2 = d_e2+ 2h_aecos₂ =225+2x2,8xcos72,39=227 мм

4.3.11. Определение среднего окружного модуля.

Расчет произведем по ГОСТ 19624-74 (таблица 3.11., источник №1, стр.50). Но прежде определим среднее конусное расстояние.

Для шестерни: R₁ = R_e-0,5b₁ = 118 – 0,5·36 = 100 мм

Для колеса: R₂ = R_e-0,5b₂ = 118 – 0,5·34 = 101 мм

средний окружной модуль:

Для шестерни: m₁ = m_e·R₁/R_e = 2,848·112/118= 2,41 мм

Для колеса: m₂ = m_e·R₂/R_e = 2,848·111,5/118= 2,69 мм

4.3.12. Определение коэффициента ширины шестерни по среднему диаметру

Коэффициент ширины шестерни по среднему диаметру:

ψ_bd=b₁/d₁=36/61=0,59=0,6

4.3.13. Определение окружной скорости вращения шестерни и колеса.

Рассчитаем окружную скорость вращения по формуле

4.4. Проверочный расчет на выносливость по контактным напряжениям.

Выполним проверочный расчет по формуле (3.27.), источник №1, стр. 47.

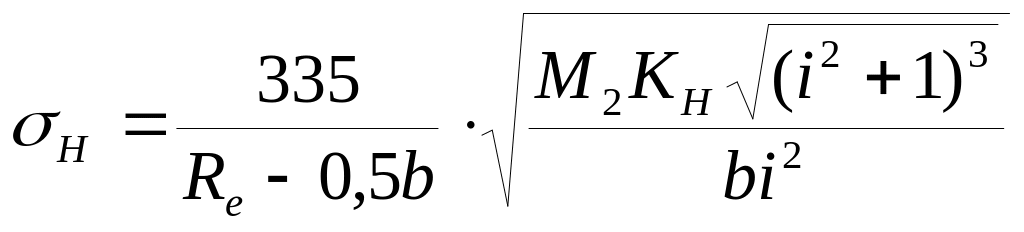
Где К_Н – есть коэффициент, определяемый соотношением (см. стр. 49, источник №1):

При заданной твердости стали (НВ < 350) и несимметричном расположении колес относительно опор (сказывается влияние того, что со стороны клиноременной передачи действует сила давления на ведущий вал, вызывающая его деформацию и ухудшающая контакт зубьев) примем значение коэффициента К_Нβ, учитывающего неравномерность распределения нагрузки по ширине венца, равное: К_нβ = 1,24 (источник №1, стр. 39, табл. 3.5).

У нас прямозубые колеса следовательно К_Нα =1.

Значение динамического коэффициента принимают в зависимости от окружной скорости, твердости поверхности зубьев НВ и степени точности 8. (источник №1, табл. 3.6, стр. 40). Выберем К_нv = 1,05.

Подставляя числовые данные, получим:

.

После определения численного значения коэффициента К_Н мы можем определить значение контактного напряжения:

= 427 МПа (см. 4.2.1.)

>

Проверка выполнена успешно.

Посчитаем недогруз системы

4.5. Проверочный расчет по напряжениям изгиба.

4.5.1. Определение коэффициента нагрузки K_F

Т.к. в редукторе будет использоваться коническая передача, то степень точности возьмем равной 8. Расчет проведем по формуле 3.22. (источник №1, стр. 41). Значение

= 1,62 (таблица 3.7, источник №1, стр. 43). Значение K_Fv = 1,25 (таблица 3.8, источник №1, стр. 43).

Итак, K_F = ·K_Fv= 1,62·1,25 = 2,025

4.5.2. Определение окружной силы в зубчатом зацеплении.

Определим окружную силу по формуле

F_t1 = 2M₁/d₁ = 2·36,88·1000/61 = 1209 H

F_t2 = 2M₂/d₂ = 2·111,4·1000/192 = 1160H

4.5.3. Определение коэффициента формы зуба.

Значение Y_F1 = 3,90 z₁ = 25 (Источник №1, стр. 42).

Значение Y_F2 = 3,61 z₂ = 79 (Источник №1, стр. 42)..

4.5.4. Определение коэффициента Y_β.

Коэффициент Y_β может быть определен соотношением:

4.5.5. Определение коэффициента К_Fα.

Коэффициент К_Fα определяется по формуле:

;

где среднее значение коэффициента торцевого перекрытия ε_α принимается равным 1,5; степень точности n = 8.

Откуда: .

4.5.6. Определение допускаемых напряжений при проверке зубьев на выносливость по напряжениям изгиба.

Коэффициент безопасности: [S_F] = [S_F]` [S_F]``.

Согласно источнику [1] (табл. 3.9, стр. 44) коэффициент [S_F]`, учитывающий нестабильность свойств материала зубчатых колес, следует принимать равным: [S<sub>F</sub>]` = 1,75. Коэффициент [S_F]``, учитывающий способ получения заготовки зубчатого колеса, для поковок и штамповок следует принимать равным: [S<sub>F</sub>]`` = 1.

Следовательно, [S_F] =1,75 1 = 1,75.

Из таблицы 3.9. (источник №1, стр. 45) получаем допускаемые напряжения при расчете зубьев на выносливость:

Для шестерни:

Для колеса:

По формуле (3.24), источник №1, стр. 43, получаем:

Для шестерни:

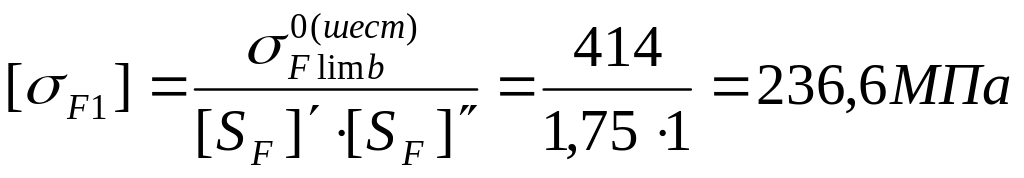
Для колеса: