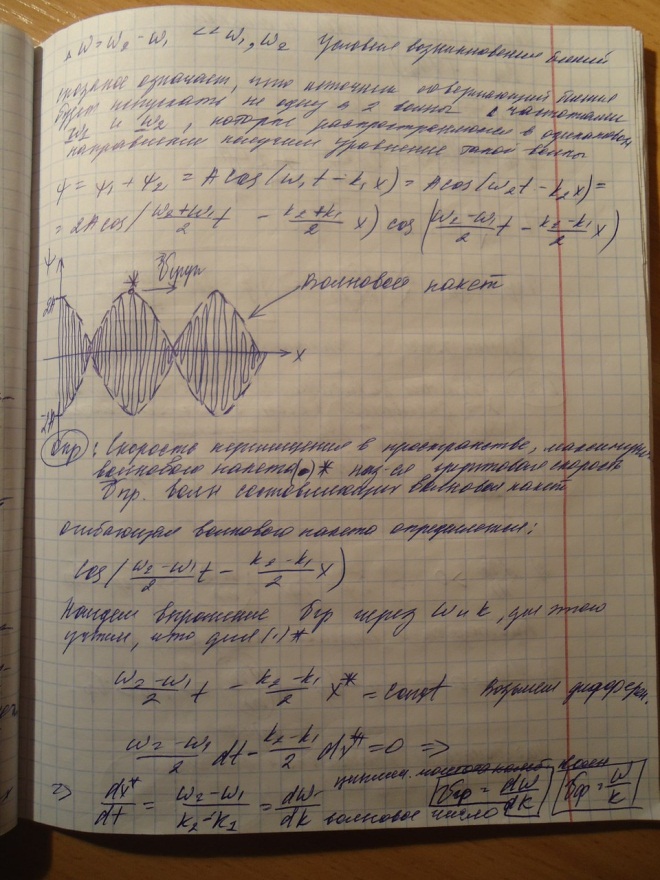
Билет 16. Дифф. Волновое уравнение, его решение

В многомерном случае однородное волновое уравнение записывается в виде

где   — оператор Лапласа,   —неизвестная функция,   — время,   — пространственная переменная,   — фазовая скорость.

В одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде

Оператор Д’Аламбера

Разность   называется оператором Д’Аламбера и обозначается как   (разные источники используют разный знак). Таким образом, с использованием оператора Д'Аламбера (даламбертиана) однородное волновое уравнение записывается как:

Решение волнового уравнения.

Формула Д'Аламбера

Решение одномерного волнового уравнения (здесь   — фазовая скорость)

 (функция   соответствует вынуждающей внешней силе)

с начальными условиями имеет вид Интересно заметить, что решение однородной задачи , имеющее следующий вид

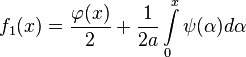
может быть представлено в виде где 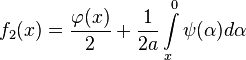В таком случае говорят, что решение представлено в виде суммы бегущих волн, а функции   и   - это профили волн, бегущих, соответственно, влево и вправо. В рассматриваемом случае профили волн со временем не изменяютс я.