Билет 9.Энергия гармонических колебаний

        При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W: (Скорость тела v = ds/dt

Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы

для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях:    2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.  3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

        В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.

        Сравнивая эти формулы, можно сделать следующие выводы:

1. Полная энергия в контуре остается неизменной: 

2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре.  3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.

        Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.

Билет 10. . Дифф.Уравнение затухающих колебаний, его решение. Периодическое и апериодическое движение.

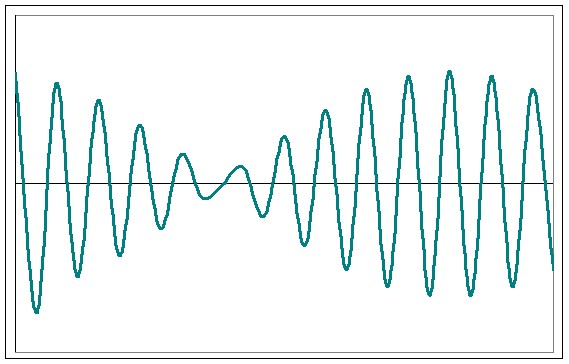
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.

Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяется. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями.

Дифференциальное уравнение свободных затухающих колебаний линейной системы

где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде

 (7.1) где u=u(t).

После нахождения первой и второй производных и их подстановки в (1) получим

Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен:

(7.2)

Тогда получим уравнение решением которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий

 где 

Период затухающих колебаний с учетом формулы (7.2) равен

 

Если A(t) и A(t+Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его логарифм

— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых во время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротности, которая при малых значениях логарифмического декремента равна

Среди всевозможных совершающихся вокруг нас механических движений часто встречаются повторяющиеся движения. Любое равномерное вращение является повторяющимся движением: при каждом обороте всякая точка равномерно вращающегося тела проходит те же положения, что и при предыдущем обороте, причем в такой же последовательности и с такой же скоростью. В действительности не всегда и не при всяких условиях повторение совершенно одинаково. В одних случаях каждый новый цикл очень точно повторяет предыдущий, в других случаях различие между следующими друг за другом циклами может быть заметным. Отклонения от совершенно точного повторения очень часто настолько малы , что ими можно пренебречь и считать движение повторяющимся вполне точно, т.е. считать его периодическим. Периодическим называется повторяющееся движение, у которого каждый цикл в точности воспроизводит любой другой цикл. Продолжительность одного цикла называется периодом. Очевидно, период равномерного вращения равен продолжительности одного оборота.

АПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ

частный случай затухающего колебательного движения, при котором собственно колебательное движение развиться не может и материальная точка или система таких точек, выведенная из положения своего устойчивого равновесия, приближается к последнему с убывающей скоростью без колебаний.