
- •Лекция 4. Течение жидкости в колесе центробежного насоса. Кпд насосов; удельная работа колёс с конечным и бесконечным числом лопастей; определение наружного диаметра колеса центробежного насоса.
- •4.1. Кпд насосов.
- •4.2. Течение жидкости в колесе центробежного насоса.
- •Общие сведения о структуре потока во входном и выходном сечениях колеса.
- •Определение удельной работы колеса с конечным числом лопаток.
- •Определение диаметра колеса центробежного насоса при известном значении действительной удельной работы колеса.
4.2. Течение жидкости в колесе центробежного насоса.
Общие сведения о структуре потока во входном и выходном сечениях колеса.
При работе центробежного колеса частицы жидкости, попадая на входные кромки лопасти, вовлекаются в окружное движение. Если при этом скорость кромок лопастей на диаметре D1 (или радиусе R1) равна u1 (см. рис. 3), то соответственно эта скорость рассматривается как переносная составляющая скорости частиц жидкости в точке соприкосновения с лопастью. Из-за окружного движения частицы жидкости одновременно начинают двигаться по радиусу под действием центробежной силы, возникающей вследствие кругового движения. Если считать число лопастей бесконечно большим (z = ∞), а их толщины бесконечно малыми, то движение жидкости в рассматриваемой точке межлопастного канала такого колеса будет направлено строго по касательной к профилю лопасти в этой точке. Движение по профилю лопасти считается относительным движением жидкости с относительной скоростью w, вектор которой направлен по касательной к профилю лопасти в рассматриваемой точке канала. Соответственно на входной кромке лопасти эта составляющая скорости равна w1∞. Знак ∞ используется здесь для обозначения всех скоростей, поскольку движение жидкости рассматривается в соответствии со струйной теорией, для колеса с бесконечным числом лопаток. Абсолютная скорость c1∞ движения частиц жидкости будет равна векторной сумме переносной и относительной составляющих. Радиальная составляющая скорости движения частиц определяется как проекция абсолютной скорости на радиус и будет равна cm1∞. Окружная составляющая абсолютной скорости определяется как её проекция на перпендикуляр к радиусу или на вектор скорости u1∞. На входной кромке лопасти она равна cu1∞.
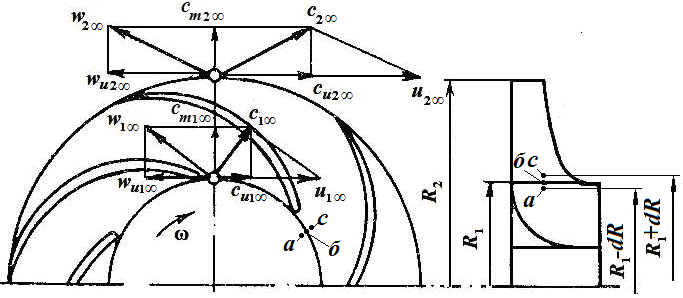
Рис.3. Треугольники скоростей на входе и выходе колеса с бесконечным числом лопастей
На выходе из колеса вектор относительной скорости направлен по касательной к профилю лопасти и равен w2∞. В сумме с окружной составляющей u2∞ он определяет величину абсолютной скорости c2∞ на выходе из колеса с бесконечным числом лопастей. Окружная составляющая абсолютной скорости на выходе из колеса равна cu2∞. Использование струйной теории позволяет просто строить треугольники скоростей на входе и выходе, учитывая только особенности геометрии лопастей.
В реальных насосах число лопастей конечно. Соответственно построение треугольников скоростей здесь должно быть сопряжено с учётом реального движения жидкости в межлопастных каналах. Основными факторами, влияющими на изменения закона движения жидкости в межлопастных каналах, являются: циркуляционный вихрь в пространстве между лопатками (см. рис. 4) и разница давлений на лобовой и тыльной поверхностях лопаток (см. рис. 7). Возникновение вихря можно объяснить на основе рассмотрения процесса, происходящего при вращении вокруг оси закрытого объёма абсд, заполненного жидкостью. При вращении такого объёма жидкость, обладающая свойством инерции покоя, стремится сохранить в пространстве своё прежнее положение. В то же время стенки объёма абсд, придя во вращательное движение, начинают двигаться относительно жидкости, сохраняющей первоначальное положение. Для наблюдателя, расположенного на внутренней стенке объёма, двигаться будет не стенка, а жидкость относительно стенки. Иными словами, имеет место движение жидкости относительно стенки, как и движение стенки относительно жидкости в соответствии с принципами относительности. В таком относительном движении жидкость без трения вращается относительно стенок в вихре, имеющем ту же угловую скорость, что и скорость вращения колеса, но противоположно направленном. Если теперь раскрыть объём абсд по линиям да и бс, то вихревое течение наложится на относительное течение потока через межлопастное пространство (связанное с расходом жидкости), в результате чего рассмотренный нами вихрь будет частично разрушен, но при этом он окажет своё влияние на направление вектора относительного движения потока.
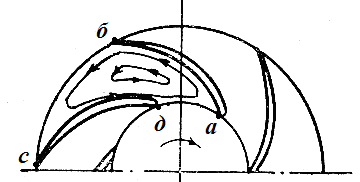
Рис.4. К вопросу об образовании циркуляционного вихревого движения в межлопаточном пространстве
Описанные процессы будут происходить в межлопастных пространствах колёс с любыми формами лопаток, в том числе и с чисто радиальными лопатками. На рис. 5 показано взаимодействие расходной и циркуляционной составляющих в межлопастном канале колеса с радиальными лопатками (радиальные здесь выбраны для упрощения рисунка) при образовании результирующей эпюры скоростей и формировании нового направлении результирующего вектора относительной скорости движения потока на выходе из колеса. Как видно из рис. 5а, при отсутствии вращательного движения вектор относительной скорости на выходе из колеса w2 направлен строго по профилю лопастей (в данном случае по радиусу). При отсутствии расходной составляющей и при вращении колеса этот вектор направлен перпендикулярно радиусу и обратно направлению вращения (рис. 5б).
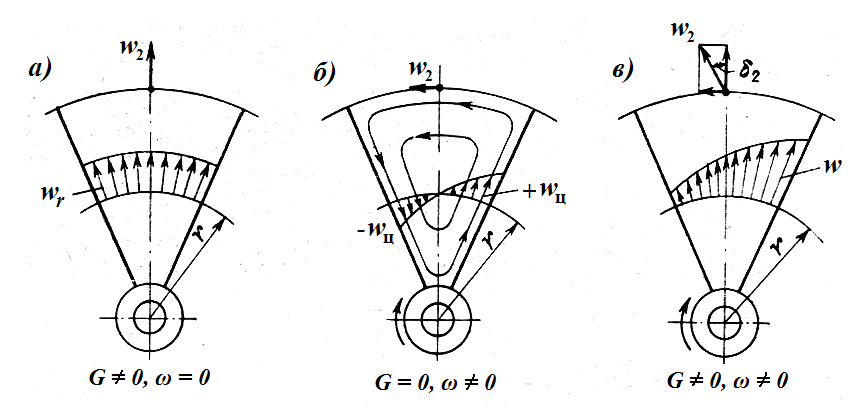
Рис.6. Схема взаимодействия расходной и циркуляционной составляющей скорости потока при
образовании результирующей эпюры скоростей: а – расходная составляющая; б – циркуляционная
составляющая; в – результирующая эпюра
При одновременном присутствии расходной и циркуляционной составляющей (вращении колеса) возникает результирующая эпюра, главный вектор которой, w2, отклоняется от направления, соответствующего профилю лопаток на выходе, в сторону, противоположную вращению колеса.
Разность давлений на лобовой (А) и тыльной (Б) (см. рис.7) поверхностях колеса возникает естественным образом при вращении колеса и при воздействии лопастей на водяной поток. На тыльной стороне давление ниже, а на лобовой выше. Если взять точки А и Б на одном радиусе r то, в соответствии с уравнением Эйлера, энергия потока жидкости в этих обеих точках будет одинаковой. В то же время, если выделить радиальную струйку жидкости вблизи точки А, где давление выше, то в соответствии с уравнением Бернулли радиальная скорость рядом с этой точкой в ней будет меньше, чем в струйке рядом с точкой Б, с тыльной поверхности лопасти, где давление ниже. По уравнению Бернулли, при равных значениях энергии в рассматриваемых сечениях, с ростом давления падает скорость потока и наоборот. Отмеченное обстоятельство объясняет особенности эпюры относительных скоростей w, которая зеркально отображает эпюру давлений в межлопастном канале (см. рис.7), если учитывать только влияние разностей давлений по обе стороны лопатки на структуру потока. Понятно также, что суммирующий вектор эпюры относительных скоростей w на выходе из колеса, w2, будет отклоняться противоположно направлению вращения колеса.
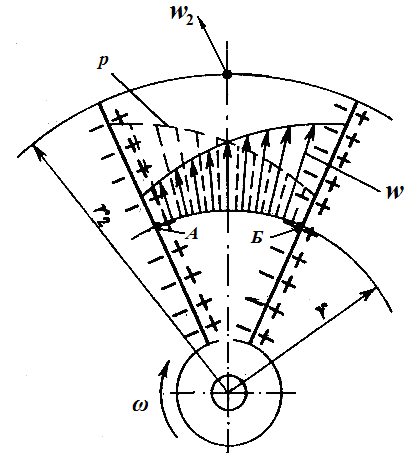
Рис.7. Распределение давлений и относительных скоростей
в канале центробежного колеса под влиянием разности давлений по обе стороны лопасти
Таким образом, оба отмеченных выше фактора действуют в одном направлении на отклонение результирующего вектора относительной скорости потока на выходе из колеса от направления касательной к лопасти на наружном диаметре колеса. Под действием этих факторов вектор действительной относительной составляющей скорости потока на выходе из колеса w2 не будет совпадать с касательной к профилю лопасти на наружном диаметре. Он должен отклоняться от касательной против направления вращения колеса на угол, который очевидно зависит от числа лопаток, их ориентации на выходе и интенсивности воздействия лопасти на поток жидкости.
Дальнейшее изучение треугольников скоростей на входе и выходе лопастей центробежного колеса необходимо для определения конструктивных размеров колеса в зависимости от заданной удельной работы насоса. Кроме того, изучение треугольников скоростей необходимо для понимания и учёта некоторых дополнительных свойств центробежного насоса, в частности, его кавитационных качеств.
Рассмотрим
треугольники скоростей на выходе из
колеса центробежного насоса при
бесконечно большом числе лопаток колеса.
Для рассмотрения выберем два сечения:
первое на радиусе R2,
а второе на радиусе R2+dR,
бесконечно близком к первому. Все
скорости треугольника в первом сечении
обозначены буквами без штрихов. Во
втором сечении – со штрихами. Построение
треугольника без штрихов совершенно
аналогично тому, как это описано ранее,
и поэтому не нуждается в пояснениях.
Напомним только, что в нём скорость w2∞
ориентирована
по касательной к средней линии профиля
лопасти на выходе, т.е. под углом β2
к касательной к окружности колеса в
точке выхода потока из колеса. Угол β2
называется углом установки лопасти на
выходе. После выхода потока из колеса
он попадает в пространство, свободное
от загромождения лопастями. Соответственно
увеличивается площадь сечения потока.
По уравнению расхода увеличение сечения
ведёт к уменьшению скорости. В связи с
этим скорость
![]() будет
уменьшена. Скорость cu2∞
здесь определяет величину удельной
энергии, сообщаемой лопастями потоку,
в соответствии с уравнением Эйлера. Эта
энергия сохраняется в потоке после
выхода из колеса и может считаться
неизменной, если величина dR
стремится к нулю. В этом случае cu2∞
для обоих треугольников можно считать
одинаковой. Тогда конец вектора абсолютной
скорости потока на выходе из колеса
будет
уменьшена. Скорость cu2∞
здесь определяет величину удельной
энергии, сообщаемой лопастями потоку,
в соответствии с уравнением Эйлера. Эта
энергия сохраняется в потоке после
выхода из колеса и может считаться
неизменной, если величина dR
стремится к нулю. В этом случае cu2∞
для обоих треугольников можно считать
одинаковой. Тогда конец вектора абсолютной
скорости потока на выходе из колеса
![]() должен оставаться на перпендикуляре к
скорости u2,
проведенном через конец вектора cu2∞.
В то же время он должен находиться на
перпендикуляре, проведенном из конца
вектора
.
Определив таким образом положение конца
вектора
,
можно провести вектор
должен оставаться на перпендикуляре к
скорости u2,
проведенном через конец вектора cu2∞.
В то же время он должен находиться на
перпендикуляре, проведенном из конца
вектора
.
Определив таким образом положение конца
вектора
,
можно провести вектор
![]() ,
поскольку начала
этих векторов сходятся в одной точке.
Следует отметить, что из всех рассмотренных
особенностей последнего треугольника
скоростей самой важной является та, что
в этом треугольнике окружная составляющая
абсолютной скорости cu2∞
остаётся такой же, как и в
сечении на выходном диаметре колеса.
,
поскольку начала
этих векторов сходятся в одной точке.
Следует отметить, что из всех рассмотренных
особенностей последнего треугольника
скоростей самой важной является та, что
в этом треугольнике окружная составляющая
абсолютной скорости cu2∞
остаётся такой же, как и в
сечении на выходном диаметре колеса.
Этот треугольник и его особенность важны потому, что именно его выделяют далее при определении удельной работы колеса. Следует напомнить, что до сих пор рассматривалось идеальное колесо и идеальный треугольник.
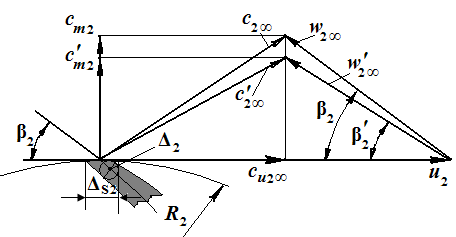
Рис. 8. Треугольники скоростей на выходе из колеса центробежного насоса при z = ∞
Если рассматривать реальное колесо с конечным числом лопастей, то на скорости потока при выходе из колеса влияют уже рассмотренные выше факторы. При постоянной скорости u2 вектор относительной скорости в таком колесе будет проходить под меньшим углом к u2, чем β2. Этот угол называют β2ср – осреднённый угол направления результирующего вектора относительной скорости w2 реального потока на выходе из колеса. Выходной треугольник скорости для реального колеса, совмещённый с выходным треугольником скоростей для идеального колеса на радиусе R2+dR показан на рис.9. Из рисунка видно, что величина окружной составляющей абсолютной скорости cu2 для реального колеса меньше, чем соответствующая величина cu2∞ для колеса с бесконечным числом лопастей. Это значит, что в соответствии с уравнением Эйлера реальное колесо будет сообщать потоку жидкости меньшую удельную работу, чем идеальное колесо.
Входные треугольники скоростей для насосов, в которых нет устройств, закручивающих поток жидкости перед колесом, не рассматриваются для определения удельной работы колеса. Напомним, что при определении удельной работы колеса выделяются два сечения. Первое проводится по радиусу R1-dR, а второе – по радиусу R2+dR. В первом сечении поток, не имеющий закрутки, не имеет окружной составляющей абсолютной скорости, т.е. для него cu1= 0, а значит входной треугольник и его составляющие для оценки удельной работы колеса не нужны. Тем не менее, входной треугольник скоростей необходим при конструировании входного участка колеса и оценки его кавитационного качества. С этими целями следует рассмотреть треугольники скоростей на входе в колесо в трёх сечениях: на радиусе R1–dR, на радиусе R1 и на радиусе R1+dR (см. рис. 3, точки а, в, с и рис.10). Пусть схема колеса насоса при этом соответствует рис.3. Следует отметить, что для всех выбранных сечений воздействие лопастей на поток таково, что отсутствует разница между моделью колеса с конечным и бесконечным числом лопастей.
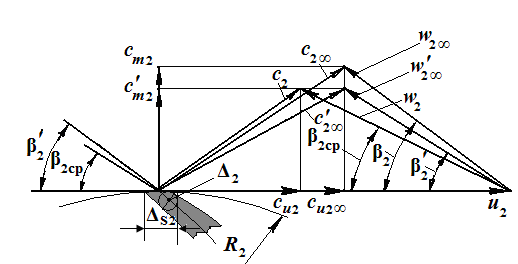
Рис. 9. Совмещённые треугольники скоростей на выходе из колеса центробежного насоса при z = ∞ и z ≠∞
Действительно, возникновение вихревых течений и разностей давлений на поверхностях лопастей связано с течением потока внутри колеса. Именно эти явления обуславливают существенные разницы в поведении двух моделей. На входе этих явлений нет, а значит, входные треугольники колёс с бесконечным и конечным числом лопастей будут идентичными с позиций тех методов оценки процессов течения жидкости в колесе, которые применяются в данном случае.
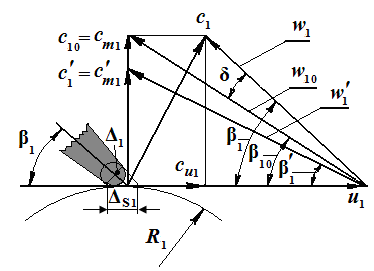
Рис. 10. Совмещённые треугольники скоростей на входе в колесо насоса
В первом сечении
(точка а,
рис3) абсолютная скорость потока
![]() направлена
строго по радиусу, поскольку закрутка
потока перед колесом отсутствует. В
этом сечении скорость частиц жидкости
относительно входной кромки колеса,
которая движется с окружной скоростью
u1,
равна
направлена
строго по радиусу, поскольку закрутка
потока перед колесом отсутствует. В
этом сечении скорость частиц жидкости
относительно входной кромки колеса,
которая движется с окружной скоростью
u1,
равна
![]() .
Эта скорость определяется векторным
вычитанием
.
Эта скорость определяется векторным
вычитанием
![]() .
Скорость
может иметь также иное наименование,
соответствующее традиционному
рассмотрению этого треугольника. В этом
случае она обозначается как
.
Скорость
может иметь также иное наименование,
соответствующее традиционному
рассмотрению этого треугольника. В этом
случае она обозначается как
![]() ,
где индекс «m»
употребляется для выделения радиального
направления векторов. Во втором сечении
(точка б,
рис 3), строго на радиусе R1,
предполагается, что поток будет
загромождён кромками лопастей, каждая
из которых в радиальном направлении
создаёт площадку препятствия с окружным
размером, равным ΔS1.
В связи с этим произойдёт увеличение
абсолютной скорости потока на входе до
c10,
которая в данном случае также может
обозначаться как cm1.
Относительная скорость потока в этом
сечении изменит своё направление и
будет соответствовать w10.
Если профиль лопасти в этом сечении
направить строго по линии w10,
то гидродинамические потери при обтекании
входного участка в таком случае будут
минимальными. Угол установки лопасти
и угол направления относительной
скорости тогда будут равны β10,
который носит название безударного
угла входа. Такое
конструктивное решение возможно и
целесообразно для насосов, которые
всегда будут работать при расходах
меньших или равных расчётному. В то же
время ряд насосов выпускается с условием,
что они могут работать на режимах с
расходами, существенно превышающими
расчётный. Если принять, что на расчётном
режиме скорость потока на входе равна
c10,
то для больших расходов скорость потока
на входе превысит c10,
а угол, под которым будет проходить
вектор относительной скорости на входе
w1,
будет превышать β10.
На таких режимах будет происходить
отрывное обтекание входной кромки
лопасти и возрастание гидродинамических
потерь. Величина этих потерь будет
возрастать пропорционально квадрату
скорости, соответственно для режимов
высоких расходов их влияние будет весьма
существенным. Кроме того, для этих
режимов увеличится падение давления
на входе. Этот фактор, в совокупности с
фактором интенсивного вихреобразования
в области всасывания насоса, может
привести к образованию паровых пузырьков
в областях с низкими давлениями.
Парообразование или холодное вскипание
жидкости на входе в насос приводит к
появлению так называемых кавитационных
явлений. В зависимости от интенсивности
вскипания они могут приводить к различным
отрицательным последствиям. В том числе
к росту шумности при работе насоса, к
износам поверхностей колеса в области
выходных кромок лопастей, к снижению
КПД насоса, а также к кавитационному
срыву. Кавитационный срыв – это аварийное
прекращение подачи насоса без возможности
её возобновления до остановки двигателя
насоса и последующего изменения режима
его работы. Чтобы снизить вероятность
проявления таких последствий, угол
установки лопасти колеса на входе β1
для насосов, которые могут работать на
режимах с расходами, превышающими
расчётный, делают большим, чем β10.
Разность угла установки лопасти и угла
безударного входа называют углом атаки
и обозначают δ. Считается, что введение
угла атаки до 15о
мало снижает КПД насоса на расчётном
режиме. Рассмотрим движение жидкости
в третьем по её ходу сечении (на радиусе
R1+
dR,
точка с
на рис.3).
Если лопатки на входе установлены под
углом β1>
β10,
то они заставят жидкость двигаться в
относительном движении по направлению
профиля лопаток, т.е. под углом β1,
по отношению к окружной скорости.
Радиальная составляющая абсолютной
скорости в данном сечении остаётся
неизменной и равной cm1.
Учитывая то, что известны cm1
и β1
можно построить треугольник скоростей
в третьем сечении, где концы векторов
абсолютной скорости c1
и относительной
скорости на входе w1
будут найдены на пересечении перпендикуляра
к концу вектора cm1
и линии, направленной под углом β1.
В этом
сечении абсолютная скорость потока на
входе уже отклонена от радиального
направления и имеет окружную составляющую,
равную cu1.
Следует иметь в виду, что появление
окружной составляющей у входной скорости
в рассматриваемом сечении не является
причиной учёта этой составляющей в
уравнении Эйлера, если перед входом
жидкости в колесо поток не закручен с
помощью какого-либо устройства.
,
где индекс «m»
употребляется для выделения радиального
направления векторов. Во втором сечении
(точка б,
рис 3), строго на радиусе R1,
предполагается, что поток будет
загромождён кромками лопастей, каждая
из которых в радиальном направлении
создаёт площадку препятствия с окружным
размером, равным ΔS1.
В связи с этим произойдёт увеличение
абсолютной скорости потока на входе до
c10,
которая в данном случае также может
обозначаться как cm1.
Относительная скорость потока в этом
сечении изменит своё направление и
будет соответствовать w10.
Если профиль лопасти в этом сечении
направить строго по линии w10,
то гидродинамические потери при обтекании
входного участка в таком случае будут
минимальными. Угол установки лопасти
и угол направления относительной
скорости тогда будут равны β10,
который носит название безударного
угла входа. Такое
конструктивное решение возможно и
целесообразно для насосов, которые
всегда будут работать при расходах
меньших или равных расчётному. В то же
время ряд насосов выпускается с условием,
что они могут работать на режимах с
расходами, существенно превышающими
расчётный. Если принять, что на расчётном
режиме скорость потока на входе равна
c10,
то для больших расходов скорость потока
на входе превысит c10,
а угол, под которым будет проходить
вектор относительной скорости на входе
w1,
будет превышать β10.
На таких режимах будет происходить
отрывное обтекание входной кромки
лопасти и возрастание гидродинамических
потерь. Величина этих потерь будет
возрастать пропорционально квадрату
скорости, соответственно для режимов
высоких расходов их влияние будет весьма
существенным. Кроме того, для этих
режимов увеличится падение давления
на входе. Этот фактор, в совокупности с
фактором интенсивного вихреобразования
в области всасывания насоса, может
привести к образованию паровых пузырьков
в областях с низкими давлениями.
Парообразование или холодное вскипание
жидкости на входе в насос приводит к
появлению так называемых кавитационных
явлений. В зависимости от интенсивности
вскипания они могут приводить к различным
отрицательным последствиям. В том числе
к росту шумности при работе насоса, к
износам поверхностей колеса в области
выходных кромок лопастей, к снижению
КПД насоса, а также к кавитационному
срыву. Кавитационный срыв – это аварийное
прекращение подачи насоса без возможности
её возобновления до остановки двигателя
насоса и последующего изменения режима
его работы. Чтобы снизить вероятность
проявления таких последствий, угол
установки лопасти колеса на входе β1
для насосов, которые могут работать на
режимах с расходами, превышающими
расчётный, делают большим, чем β10.
Разность угла установки лопасти и угла
безударного входа называют углом атаки
и обозначают δ. Считается, что введение
угла атаки до 15о
мало снижает КПД насоса на расчётном
режиме. Рассмотрим движение жидкости
в третьем по её ходу сечении (на радиусе
R1+
dR,
точка с
на рис.3).
Если лопатки на входе установлены под
углом β1>
β10,
то они заставят жидкость двигаться в
относительном движении по направлению
профиля лопаток, т.е. под углом β1,
по отношению к окружной скорости.
Радиальная составляющая абсолютной
скорости в данном сечении остаётся
неизменной и равной cm1.
Учитывая то, что известны cm1
и β1
можно построить треугольник скоростей
в третьем сечении, где концы векторов
абсолютной скорости c1
и относительной
скорости на входе w1
будут найдены на пересечении перпендикуляра
к концу вектора cm1
и линии, направленной под углом β1.
В этом
сечении абсолютная скорость потока на
входе уже отклонена от радиального
направления и имеет окружную составляющую,
равную cu1.
Следует иметь в виду, что появление
окружной составляющей у входной скорости
в рассматриваемом сечении не является
причиной учёта этой составляющей в
уравнении Эйлера, если перед входом
жидкости в колесо поток не закручен с
помощью какого-либо устройства.
