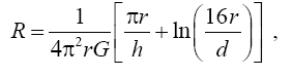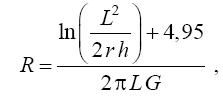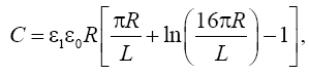Додаток б. Варіанти завдань для підготовки до модульного контролю по темі «Розв’язання нелінійних рівнянь»
Нижче приведені варіанти завдань. Кожне з них включає варіанти, що відрізняються один від одного набором даних. Всі параметри у формулах, якщо не обумовлене інше, слід записувати в системі СІ.
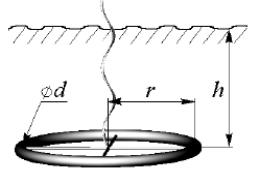
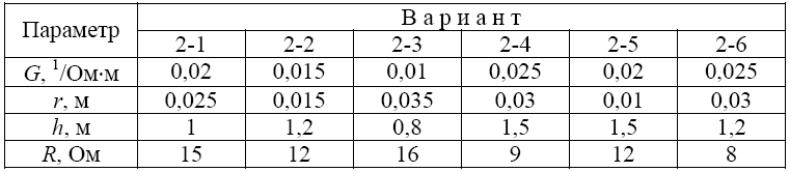
Завдання 1. Заземлітель у формі кільця радіусом r розташований в грунті на глибині h. Його сопротивление при h >> r розраховується по формулі:
|
|
де π = 3,14., G - електропровідність грунту, d - діаметр провідника з якого виготовлено кільце.
Задавшись параметрами h і d, вказаними в таблиці, а також прийнявши G = 0,03 1/Ом·м, знайдіть радіус r, що забезпечує необхідне сопротивление заземлення R .
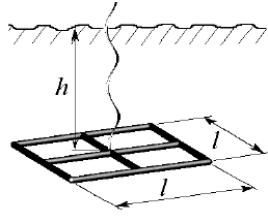
Завдання 2. Заземлітель, виготовлений у вигляді грат прямокутної форми з металевих труб|, розташований горизонтально в грунті на глибині h. Опір заземлителя розраховується по формулі
|
|
де π = 3,14…, L = 6×l − сумарна довжина труб, r − радіус труб, h − глибина, G − питома електропровідність грунту.
Задавшись параметрами r = 0,01 м, h (із таблиці), визначите розмір l, відповідний необхідному сопротивлению R.
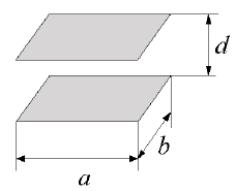
Завдання 3. Електрична ємкість системи двох паралельних пластин прямокутної форми (див. Малюнок) при a ≥ d і b ≥ d може бути визначена по формулі:
|
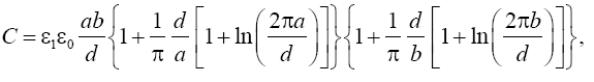
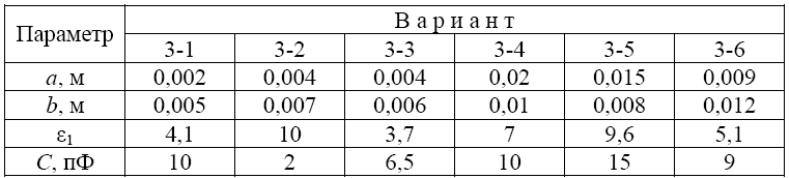
де ε1 − відносна діелектрична проникність середовища, ε0 = 8,85·10–12 Ф/м; a і b − розміри пластин; d − відстань між пластинами, π = 3,14…. Знайдіть зазор d, що забезпечує отримання необхідної ємкості C при вказаних в таблиці параметрах.
|
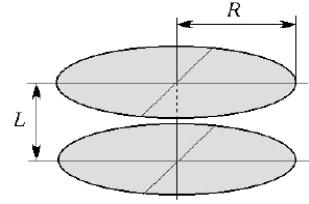
Завдання 4. Електрична ємкість двох коаксіальних плоских дисків (див. малюнок) при L/R<1 розраховується по формулі:
|
|
де ε1 − відносна діелектрична проникність середовища,
ε0 = 8,85·10–12 Ф/м, R − радіус дисків, L − відстань між дисками, π =3,14... .
Знайдіть радіус R, що задовольняє необхідному значенню ємності С, при заданих в таблиці параметрах ε1 и L .
Завдання 5. У інтегральних схемах використовують планарные конденсатори, що мають вигляд металевого диска, розташованого в круглому вирізі металізації на поверхні діелектричної підкладки (див. малюнок). Ємкість такого конденсатора визначається по формулі: |
|
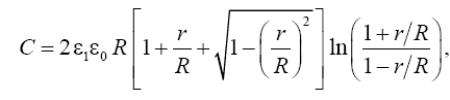
де ε1 − відносна діелектрична проникність діелектрика,
ε0 = 8,85·10−12 Ф/м, R − радіус вирізу, r – радіус диска.
Задавшись вказаними в таблиці параметрами ε1 і r, знайдіть радіус R, що забезпечує необхідну ємкість С.
Завдання 6 Для експериментально отриманої прямої гілки вольтамперної характеристики напівпровідникового діода при u < 0,6В В підібрана апроксимація у вигляді:
|
|
де ток i заданий в міліамперах, напруга u – у вольтах.
Використовуючи апроксимацію, знайдіть напругу на діоді, при якому через нього протікатиме заданий в таблиці ток i. При складанні рівняння використовуйте вказані в таблиці параметри a, b, c, d і e.
Параметр |
Варіант |
|||||
7-1 |
7-2 |
7-3 |
7-4 |
7-5 |
7-6 |
|
i,мА |
11 |
15 |
22 |
25 |
32 |
47 |
a,мА/В |
0,2 |
2,3 |
112 |
32 |
39 |
15 |
b,мА/В2 |
97 |
150 |
215 |
67 |
140 |
22 |
c,мА/В3 |
88 |
120 |
110 |
275 |
97 |
217 |
d,мА/В4 |
350 |
457 |
465 |
84 |
192 |
118 |
e,мА/В5 |
112 |
97 |
149 |
52 |
76 |
56 |
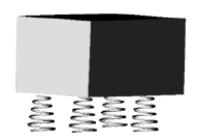
Завдання 7. Для захисту від вібрації блок літакової станції радіолокації встановлений на чотирьох амортизаторах. Система амортизації при цьому може мати до шести власних механічних резонансів, частоти яких визначаються рівнянням:
|
|
де A, B, C, D, E, F, G − коефіцієнти, що визначаються параметрами конструкції, ω – частота коливань.
Знайдіть резонансні частоти для заданих коефіцієнтів рівняння.
Параметр |
Варіант |
|||||
8-1 |
8-2 |
8-3 |
8-4 |
8-5 |
8-6 |
|
А |
0,01 |
0 |
0 |
0,1 |
1 |
0 |
B |
1 |
0,01 |
0,02 |
–20 |
0 |
0 |
C |
–78 |
1 |
0,1 |
102 |
–29900 |
1 |
D |
2,1e3 |
–1,25e3 |
–2,56e3 |
–8,98e3 |
0 |
–116 |
E |
-2,5e4 |
1,85e5 |
3,45e5 |
8,76e6 |
26400 |
4,3e3 |
F |
1,2e5 |
–8,75e6 |
–9,95e6 |
–7,5e5 |
9,12e8 |
–5,3e4 |
G |
–1,9e5 |
8,9e7 |
2,7e7 |
–3,3e8 |
–1,75e9 |
8,9e4 |