8. Классические методы решения дифференциальных уравнений

9. Операторные методы решения дифференциальных уравнений

Алгоритм решения дифференциальных уравнений операторным методом: 1. По заданному входному воздействию u(t) с помощью таблиц или интеграла Лапласа (2.3) находится его изображение U(p). 2. По дифференциальному уравнению составляется передаточная функция W(p). 3. Определяется изображение выходной переменной по выражению . 4. Определяется оригинал y(t) на основе обратного преобразования Лапласа с помощью таблиц по изображению Y(p).

Пусть дано дифференциальное уравнение:

,

где f(t) – оригинал, а  (i = 1,2,..,n) – постоянные коэффициенты. Будем искать решение этого уравнения, удовлетворяющее начальным условиям  . Обозначим изображение исходной функции  , после чего найдем изображения правой и левой частей уравнения. Получив вспомогательное уравнение, разрешим его относительно X(p) и найдем оригинал его, то есть x(t).

Пример 4. Решить дифференциальное уравнение

при начальных условиях  .

Решение. Полагая

,

получим операторное уравнение с учетом 

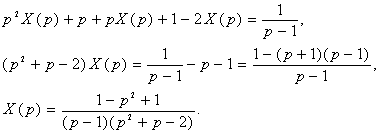
Так как  имеет корни  и  , то

.

Значит,  .

Разложим X(p) на простейшие дроби:

.

Отсюда

  .

Подставим в обе части этого тождества p=1. Тогда имеем

.

Полагая  , получим

, откуда  . Далее, подставляя найденные A и C в тождество, получим

.

Приравнивая свободные члены в обеих частях тождества, получаем уравнение для определения B:

 

а  . И следовательно,  .

10. Матричный метод решения уравнения.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с   неизвестными (над произвольным полем):

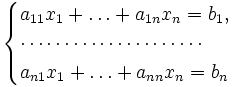
Тогда её можно переписать в матричной форме:

, где   — основная матрица системы,   и   — столбцы свободных членов и решений системы соответственно:

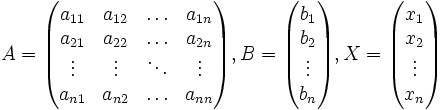
Умножим это матричное уравнение слева на   — матрицу, обратную к матрице   :  

Так как  , получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор  , действительно обратное правило: система   имеет нетривиальное (то есть ненулевое) решение только если  .

Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

11.Устоичивость автоматических систем.

Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения.

Устойчивая САУ — система, в которой переходные процессы являются затухающими.

 — операторная форма записи линеаризированного уравнения.

y(t) = y_уст(t)+y_п = y_вын(t)+y_св

y_уст(y_вын) — частное решение линеаризированного уравнения.

y_п(y_св) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть 

САУ устойчива, если переходные процессы у_n(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть   при 

Решая дифференциальное уравнение в общем случае, получим комплексные корни p_i, p_i+1 = ±α_i ± jβ_i

Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:

 , где  , 

Из полученных результатов видно, что:

• при ∀α_i<0 выполняется условие устойчивости, то есть переходный процесс с течением времени стремится к у_уст (Теорема Ляпунова 1);

• при ∃α_i>0, выполняется условие неустойчивости (Теорема Ляпунова 2), то есть 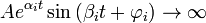  , что приводит к расходящимся колебаниям;

• при ∃α_i=0 и ¬∃α_i>0 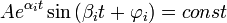 , что приводит к незатухающим синусоидальным колебаниям системы (система на границе устойчивости) (Теорема Ляпунова 3).