
ППМ_Лаб1_Алексеев_Р_Д__ИКТ-306
.doc
САНКТ ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. М. А. БОНЧ-БРУЕВИЧА
Кафедра Цифровой обработки сигналов
Лабораторная работа
«Знакомство с MATLAB. Основные объекты языка MATLAB.»
Выполнили: ст. гр. ИКТ-306
Алексеев Роман
Проверил: ________________
Санкт-Петербург
2015 год.
Цель работы:
Познакомиться с назначением и интерфейсом системы MATLAB и овладеть начальными навыками работы в режиме прямых вычислений.
Краткая теоретическая справка:
Система MATLAB — это интерактивная система, предназначенная для
компьютерного моделирования практически в любой области науки и техники.
Интерфейс MATLAB образуют следующие окна:
-
Command Window (Командное окно) — основное окно интерактивной системы MATLAB с активизированной командной строкой; Из активизированной командной строки пользователь может возвращаться к ранее введенным командам с помощью стрелок "вверх" и "вниз" на клавиатуре. Сеанс работы в окне Command Window до выхода из MATLAB называют текущей сессией.
-
Current Folder (Текущая папка) — в этом окне выводится содержимое папки, имя которой отображается в раскрывающемся списке Current Folder на панели инструментов окна MATLAB. В составе ранних версий MATLAB (до 2009 года) содержалась автоматически создаваемая текущая папка со стандартным именем work, предназначенная для хранения файлов и папок, создаваемых пользователем. В последующих версиях такая папка отсутствует. Для тех же целей предусмотрена папка MATLAB, автоматически создаваемая в папке Мои документы на Рабочем столе. Создание собственной папки в окне Current Folder выполняется с помощью контекстного меню по команде New Folder (Новая папка), и новой папке присваивается имя. Сохранение пути к собственной папке в окне Current Folder выполняется по команде контекстного меню Add to Path | Selected Folders (Добавить к пути | Выделенные папки).
-
Workspace (Рабочая область памяти) — в этом окне выводится список текущих переменных, сохраняемых в рабочей области памяти Workspace до выхода из MATLAB;
-
Command History (История команд) — в этом окне выводится построчный список объектов языка MATLAB, вводимых в ходе текущей и предшествующих сессий. Двойным щелчком левой кнопки мыши можно дублировать любую строку из окна Command History в окно Command Window.
Пользователь может произвольно менять состав активных окон с помощью команд
пункта меню Desktop (Стол).
Система оперативной помощи MATLAB включает в себя:
-
справочную систему в формате HTML (Hyper Text Markup Language — язык гипертекстовой маркировки), обращение к которой производится по команде Product Help (Помощь по продукту) в пункте меню Help окна MATLAB;
-
команду: help <стандартное имя объекта языка MATLAB>
Литература
1. Солонина А. И., Арбузов С. М. Цифровая обработка сигналов. Моделирование в
MATLAB. — СПб.: БХВ-Петербург, 2008, гл. 1—2.
2. Сергиенко А. Б. Цифровая обработка сигналов. 3-е издание — СПб.: БХВ-
Петербург, 2010, Приложения 1—2.
Задания были выполнены на следующей конфигурации:
MATLAB R2014
Windows 7 (x64)
3 GB RAM
Core 2 Duo
Nvidia GeForce GT220m
-
Запуск системы MATLAB и знакомство с ее интерфейсом. Пояснить, какие окна образуют интерфейс MATLAB.
После открытия программы MATLAB версии R2014b, нашему взору предстаёт рабочая область программы, состоящая из окон:
-
Command Window –
-
Workspace –
-
Current Folder –
Также, по умолчанию включена лента инструментов «Toolstrip». Изменить раскладку окон можно потянув или закрыв любое из них, а также через специальное меню «Layout», которое позволяет добавить в рабочую область элементы, отображение которых в данные момент отключено (например, панель вкладок «Shortcuts Tab»). Изображение стандартного интерфейса программы MATLAB R2014b приведено на рисунке “Рис.1”
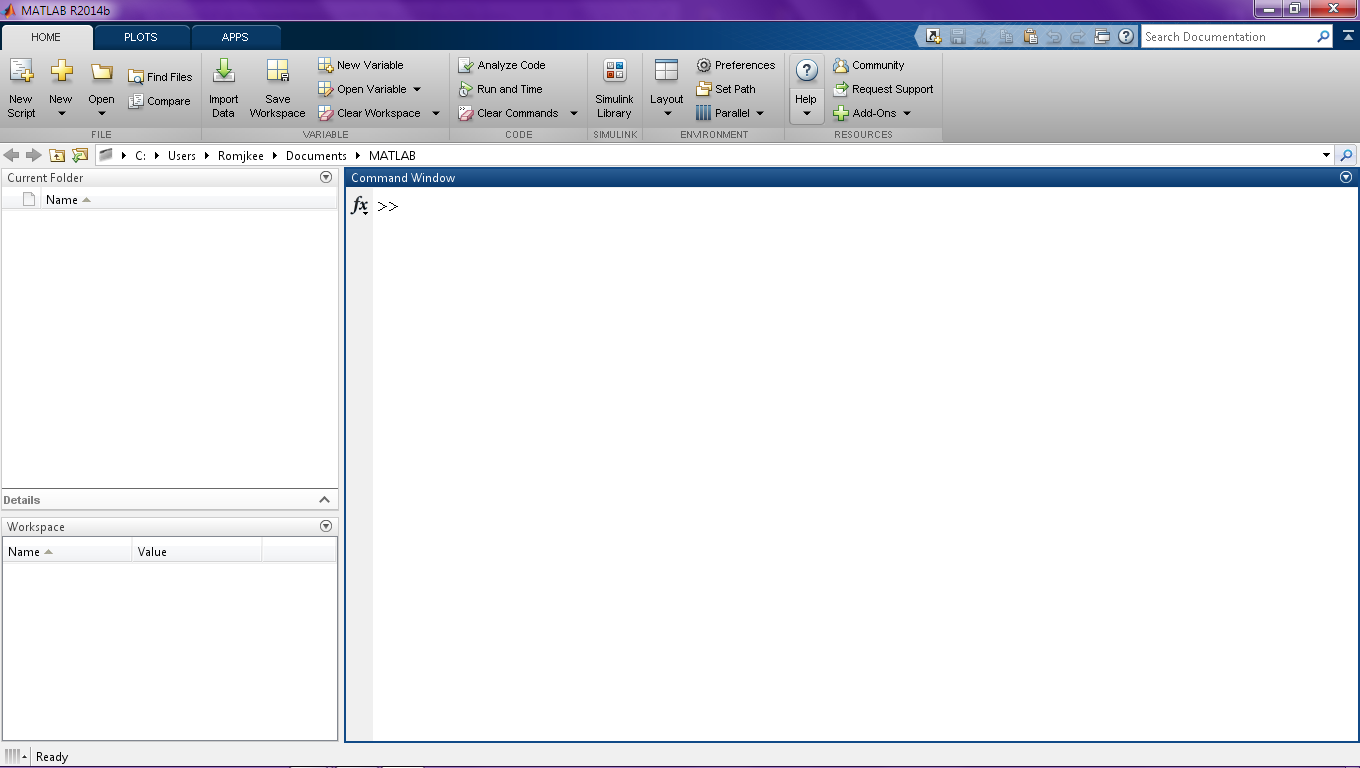
Рис.1 «Изображение
стандартного интерфейса» программы
MATLAB R2014b»
-
Знакомство со справочной системой MATLAB в формате HTML. Пояснить, как обратиться к справочной системе.
Начиная с версии MATLAB R2012b справочная система MATLAB была значительно переработана. Теперь по нажатию клавиши ‘F1’ или выборе соответствующего пункта меню в новом окне открывается раздел с документацией и поисковой строкой (“Рис.2а”). При выборе пункта «Support Website» открывается веб-страница, на которой мы можем увидеть ссылки на всё ту же документацию, примеры кода и тематический форум, посвящённый MATLAB (“Рис.2б”). Доступ к консольной версии справочной системы всё ещё предоставляется по команде «help».
Рис.2а
«Раздел с
документацией и поисковой строкой»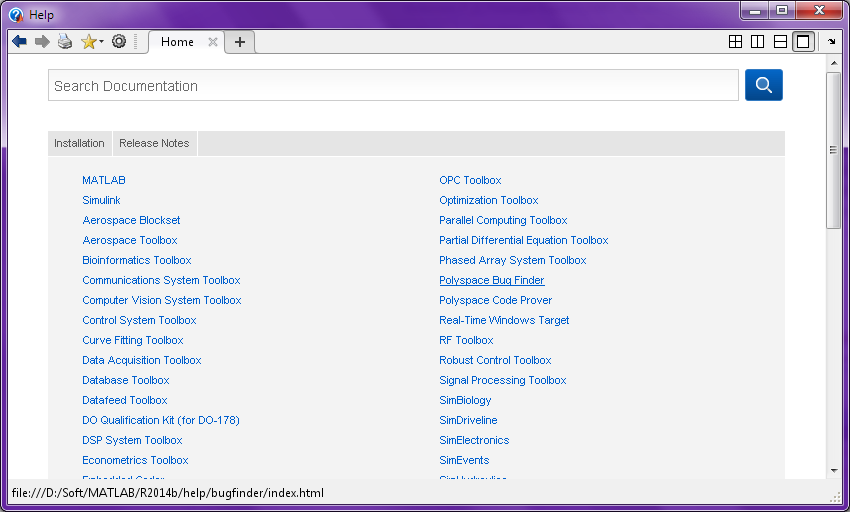

Рис.2б
«примеры кода и
тематический форум»
3.Ввод комментария в окне Command Window.
3.1 Ввести наименование лабораторной работы.
3.2 Пояснить, какой символ используется для ввода комментария.
Для ввода комментария в среде MATLAB используется символ процента («%»), который должен стоять перед текстом самого комментария (“Рис.3”).

Рис.3
«Комментарий»
-
Знакомство с командами языка MATLAB.
4.1 Выполнить команду: >> help general
4.2 Пояснить назначение и формат команды help.
4.3 О каких объектах языка MATLAB будет выдана справка?
Команда “help” помогает пользователю изучить принципы работы программы, компонента или надстройки, не выходя из «Command Window». Используется следующим образом: help <topic>, где <topic> - раздел или название компонента, по которому требуется информация. При отсутствии аргумента <topic> будет выведен список всех компонентов с ссылками на подразделы по этим компонентам. По вызову “help general” будет выведен список подразделов, необходимых начинающему пользователю среды MATLAB (например, синтаксис среды или примеры кода).
-
Очистка окна Command Window.
Пояснить, какая команда используется.
Для отчистки окна «Command Window» используется команда “clc” (Clear Commands)
-
Ввод вещественных констант
6.1 Пояснить:
6.1.1 смысл символа " ; " в конце строки;
6.1.2 какой переменной присваиваются значения вводимых констант;
6.1.3 в каком случае при вводе констант целесообразно использовать форму E;
6.1.4 в каком формате выводятся константы по умолчанию;
6.1.5 как вывести указанные константы с максимальным количеством значащих цифр в дробной части;
6.1.6 какое количество значащих цифр в дробной части будет максимальным;
6.1.7 какие форматы предусмотрены для вывода вещественных констант;
6.1.8 какую форму E называют нормализованной.
Все команды, имеющие в конце символ «;» не выводят результат на экран. Этот символ, по сути, означает переход на следующую строку. Все константы, вычисления которых не привязаны ни к одной из переменных, присваиваются автоматически создаваемой переменной “ans”. Е формой удобно пользоваться в случае, если константа, допустим, имеет большое количество нулей. Например, проще набрать 10е9 или l.0e10, чем 1000000000, а результат будет тот же самый.
Все константы, по-умолчанию, выводятся в формате “format short” - формат с автоматическим выводом в обычной форме или
нормализованной форме E с 4 значащими цифрами в дробной
части мантиссы. Для вывода константы с максимальным количеством значащих цифр в дробной части, достаточно сменить формат на “long” (командой “format long”). При этом, количество значащих цифр в дробной части будет равно 15.
Для вывода вещественных констант предусмотрено два формата: format short e и format long e.
Форму E называют нормализованной, если целая часть мантиссы содержит одну отличную от нуля значащую цифру, а порядок — три цифры.
-
Ввод комплексных констант.
7.1 Ввести следующие константы без символа ";" в конце cтроки:
0,057+0,5j
0,057+0,5i
1200000,5+56i
1200000,57857+56i
12,5+56i
12,5+0,000056i
– 0,9999999i
0i
17+10-5i
15∙10-5i
-
Пояснить:
7.2.1 в какой форме вводятся комплексные константы;
7.2.2 в какой форме вводятся их вещественные и мнимые части;
7.2.3 в каком формате выводятся комплексные константы по умолчанию;
7.2.4 какой формат целесообразно выбрать для вывода указанных констант;
7.2.5 какая из констант списка будет воспринята как вещественная.
8. Ввод логических констант.
8.1 Ввести константы true и false без символа ";" в конце строки.
8.2 Пояснить, какие значения будут выведены и какой переменной присвоены.
При вводе константы “true” переменной «ans» присваивается единица (“1”), при вводе “false” – ноль (“0”).
9. Ввод символьных констант.
9.1 Ввести константы:
9.1.1 ФИО;
9.1.2 наименование лабораторной работы.
9.2 Пояснить, как вводятся и выводятся символьные константы.
Символьные константы обрамляются одинарными кавычками. Пример ввода и вывода символьных констант показан на рисунке (“Рис.4”)

Рис.4
«Пример ввода и
вывода символьных констант»
10. Ввод векторов.
10.1 Ввести векторы — строки и столбцы — со следующими элементами:
– 0,9; 125; 0; 5+3i; 12i;
– 0,9; 125; 0; 5; 12;
1; 2; 4; 5; 12.
10.2 Пояснить:
10.2.1 какие символы используются при вводе векторов;
10.2.2 как в MATLAB воспринимаются скаляры и векторы.
При вводе векторов (- строк) используются квадратные скобки (“[ ]”) и пробелы, для разделения столбцов. Вектор (- столбцы) же, вводятся в таких же квадратных скобках, но для разделения строк служит символ “;”. Так, вектор в MATLAB можно рассматривать как матрицу размерностью 1 x n, где n – размерность вектора. Скаляр (размерностью 1х1) рассматривается и воспринимается как простая переменная.
11. Ввод матрицы.
11.1 Ввести матрицы 3 х 3 и 3 х 2 с произвольными элементами.
11.2 Пояснить, что называют размером и порядком матрицы.
Для ввода матрицы и заполнения её заведомо случайными числами используем функцию “randn” (использование: “randn (x,y), где x – число столбцов, а y – число строк матрицы”). Матрицей размеров x x y называется прямоугольная таблица чисел, содержащая x строк и y столбцов. В случае, если количество строк равно количеству столбцов, такая матрица является квадратной и порядком её называется количество строк (либо столбцов).
12. Ввод переменных.
12.1 Присвоить произвольные значения простой переменной, вектору и матрице.
12.2 Пояснить, как выбираются имена переменных и как переменные воспринимаются в MATLAB.
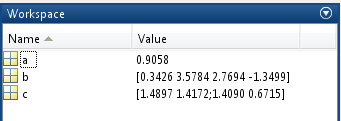
Рис.5
«Пример заполнения переменных»
Для заполнения простой переменной «a» мы воспользовались командой “a=rand”, а для заполнения вектора «b» и матрицы «c» – “b=randn(1,4)” и “c=randn(2,2)” соответственно («Рис.5»). Имя переменной составляется из последовательности латинских букв, цифр и символа подчеркивания и начинается с буквы. В MATLAB прописные и строчные буквы различаются.
13. Знакомство с особенностями ввода комплексных переменных.
13.1 Присвоить переменной i значение 5.
13.2 Присвоить переменной F значение комплексной константы 5+3i, которую ввести двумя способами: без символа умножения в мнимой части; с символом умножения.
13.3 Пояснить:
13.3.1 в каком из этих случаев и почему возникает ошибка;
13.3.2 как предотвратить возникновение ошибок в подобных случаях.
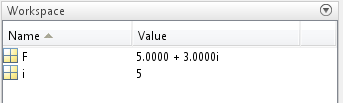
Рис.6а
«Вычисления без знака умножения»
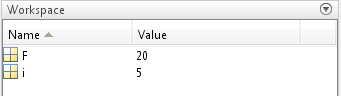
Рис.6б
«Вычисления со знаком умножения»
При выполнении команды “F=5+3i” значение “i” берётся из системной константы (мнимая единица, соответствующая корню из -1 («Рис.6а»), в то время как при вводе “F=5+3*i” тройка умножается на значение пользовательской переменной (текущее значение: 5, «Рис.6б»). Предотвратить эту ошибку достаточно легко, достаточно использовать имена переменных, которые тяжело спутать с системными, например «schetchik».
14. Знакомство со стандартными функциями с комплексным аргументом.
14.1 Присвоить переменной произвольное комплексное значение.
14.2 Вычислить модуль, аргумент, вещественную и мнимую части переменной.
14.3 Присвоить другой переменной значение комплексно сопряженной константы.
14.4 Пояснить, какие стандартные функции для этого используются.
С помощью команды “q = 2 – 3i” присвоим переменной «q» значение 2.0000 - 3.0000i. Для вычисления модуля, аргумента, вещественной и мнимой частей переменной, поочерёдно воспользуемся командами: “abs (q)”, “angle (q)”, “real (q)”, “imag (q)”. А для присвоения другой переменной значения комплексно сопряженной константы выполним: “w = conj(q)”, после которой у нас появится константа «w», равная 2.0000 + 3.0000i.
15. Ввод арифметических выражений.
15.1 Присвоить переменным a, b и c значения произвольных вещественных констант, не равных нулю.
15.2 Вычислить следующие значения :
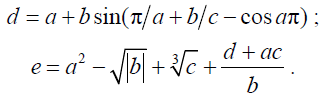
Для заполнения переменных «a, b, c» воспользуемся уже известной нам функцией «rand», а «d, e» посчитаем по формулам:
d = a+b*sin(pi/a+b/c-cos(a*pi))
e = a^2-sqrt(abs(b))+c^(1/3)+(d+a*c)/b
(«Рис.7б)
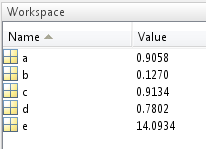
Рис.7б
Результаты вычислений
16. Ввод логических выражений.
16.1 Используя переменные предыдущего пункта, записать логическое выражение с использованием операций отношения и вычислить его значение.
16.2 Добавить в данное выражение логические операции и вычислить значение нового логического выражения.
16.3 Представить записи соответствующих логических выражений в MATLAB.
16.4 Пояснить:
16.4.1 приоритет выполнения операций;
16.4.2 какие значения может принимать логическое выражение.
17. Знакомство со стандартными переменными.
17.1 Ввести арифметические выражения, которым по умолчанию будут присвоены константы Nan и Inf.
17.2 Пояснить назначение данных констант.
Для получения Nan константы произведём вычисление 0/0, а для Inf – 1/0. NaN - Not-a-Number, не число, математическая неопределённость. Inf – математическая бесконечность.
18. Знакомство со стандартными функциями округления.
18.1 Выполнить следующие вычисления:
floor([8.2 8.5 8.7 -8.2 -8.5 -8.7])
ceil([8.2 8.5 8.7 -8.2 -8.5 -8.7])
convergent([8.2 8.5 8.7 -8.2 -8.5 -8.7])
nearest([8.2 8.5 8.7 -8.2 -8.5 -8.7])
round([8.2 8.5 8.7 -8.2 -8.5 -8.7])
fix([8.2 8.5 8.7 -8.2 -8.5 -8.7])
18.2 Привести и пояснить полученные результаты.
После выполнения команд («Рис.8») мы получаем различные виды округления, описанные в таблице «Табл.1»
Рис.8
|
fix (x) |
Табл.1 дробной части
|
|
floor (x) |
Округление в направлении -∞ — округление до ближайшего целого в сторону уменьшения
|
|
ceil (x) |
Округление в направлении +∞ — округление до ближайшего целого в сторону увеличения |
|
round (x) |
Округление до ближайшего целого — при дробной части, равной 0.5, — в сторону увеличения модуля числа |
|
nearest (x) |
Округление до ближайшего целого — при дробной части, равной 0.5, — в сторону увеличения |
|
convergent (x) |
Округление до ближайшего целого — при дробной части, равной 0.5, — в сторону ближайшего четного числа |
19. Знакомство со стандартными функциями преобразования систем счисления.
19.1 Записать произвольное целое десятичное число и преобразовать его в шестнадцатеричное и двоичное.
19.2 Выполнить обратные преобразования.
19.3 Пояснить, какие стандартные функции использовались для преобразования.
Для преобразования чисел из одной системы счисления в другую используются функции, приведённые в таблице «Табл.2». Результаты работы находятся на рисунке «Рис.9».
Табл.2
|
dec2hex(X)
|
Преобразование десятичного целого в шестнадцатеричное. Десятичное число указывается в качестве аргумента, а шестнадцатеричное выводится без апострофов с использованием заглавных букв
|
|
dec2bin(X)
|
Преобразование десятичного целого в двоичное. Десятичное число указывается в качестве аргумента, а двоичное выводится без апострофов
|
|
bin2dec(X)
|
Преобразование двоичного целого в десятичное. Двоичное число указывается в качестве аргумента в апострофах, а десятичное выводится без апострофов
|
|
hex2dec(X)
|
Преобразование шестнадцатеричного целого в десятичное. Шестнадцатеричное число указывается в качестве аргумента в апострофах с использованием |
Рис.9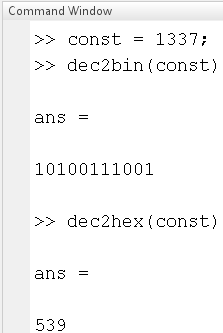
20. Сохранение переменных на диске.
20.1 Присвоить переменным A, B и C произвольные значения и сохранить их в текущей папке в файле с произвольным именем.
20.2 Пояснить:
20.2.1 какая команда используется для сохранения данных;
20.2.2 как выбирается имя файла данных;
20.2.3 какое расширение имеют файлы данных.
Для заполнения переменных «A, B, C» воспользуемся уже знакомой нам функцией «rand». Для сохранения нашей работы в файле «ABC.mat» выполним команду: Save ABC A B C
Если мы не укажем имя файла, то по файлу присваивается имя первой переменной из <списка переменных>, а расширением файла является «*.mat»
21. Знакомство с рабочим пространством памяти Workspace.
21.1 Выполнить следующие действия:
21.1.1 очистить и проверить содержимое Workspace;
21.1.2 загрузить сохраненный файл данных (см. п. 20) и вывести значение переменных A, B, C в окне Command Window;
21.1.3 проверить содержимое Workspace;
21.1.4 удалить из Workspace переменную A и проверить содержимое Workspace;
Очистка Workspace производится командой clear или в контекстном меню, после клика ПКМ в любом свободном месте Workspace. Для загрузки воспользуемся командой load ABC, которая выполняется автоматически по двойному клику в названии сохранённого файла в окне Current Folder.
22. Завершение работы MATLAB.
Завершить работу комплекса MATLAB можно командой exit или нажав крестик в правом верхнем углу окна программы.
Вывод:
После проделанной работы, мы усвоили внешний вид и основные навыки работы с новым для нас комплексом MATLAB. В ходе выполнения работы, мы поняли принципы работы комплекса, его синтаксис и основные функции, смогли узнать его основные преимущества и выявить некоторые недостатки.
Задание для самостоятельного выполнения:
1С. Ввод вещественных констант. Привести примеры ввода вещественных констант, для которых удобен обычный формат и формат E, а также тех, для которых, независимо от формы ввода, количество значащих цифр после запятой будет ограничено.
1488
14.8e8
1.4888888888888888

Рис.1C
“Ввод различных констант”
2С. Операции с комплексными константами. Ввести вещественные константы: i = 7; j = 5; и определить, в каком из следующих случаев будут выведены комплексные константы:
(5+7i)*(5+7*j)
(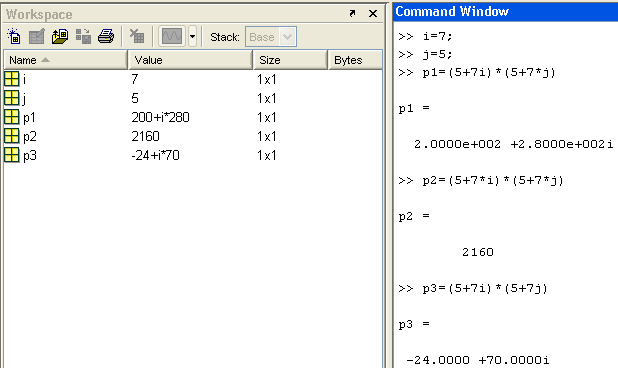 5+7*i)*(5+7*j)
5+7*i)*(5+7*j)
(
Рис.2C.1
“Операции с комплексными константами”
i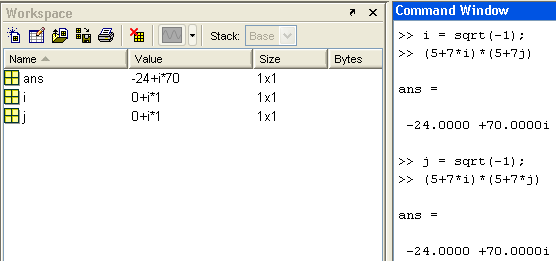 = sqrt(-1); (5+7*i)*(5+7j)
= sqrt(-1); (5+7*i)*(5+7j)
j = sqrt(-1); (5+7*i)*(5+7*j)
Рис.2C.2
“Продолжение операций с комплексными
константами”
3С. Вычисление арифметических выражений. Присвоить простым переменным a , b и c произвольные значения и записать арифметические выражения для вычислений по следующим формулам:
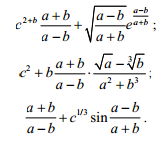

Рис.3C
“ Вычисление арифметических выражений
”
4С.
Для четырех комбинаций логических
констант х и у (00, 01, 10 и 11) вычислить
значения логического выражения (составить
таблицу истинности):
![]() ,
где символу "
" соответствует логическая операция
ИЛИ.
,
где символу "
" соответствует логическая операция
ИЛИ.

Рис.4C
“ Операции с логическими выражениями
”
5С. Операции со стандартными функциями.
Привести пример арифметического выражения с использованием стандартных функций, включая функции округления.

Рис.5C
“ Операции со стандартными функциями
”
