
- •1.Отображегия. Ф-ции. Важнейшие виды отобр. Элемент.Ф-ции и их граф.
- •2.Аксиоматика мн-ва действ.Чисел. Важнейш.Класс.Действ.Чисел.
- •3.Лемма о верхней грани числового множества.
- •4.Лемма о вложенных отрезках.
- •5. Лемма о предельной точке числового множества.
- •6. Лемма о конечном покрытии.
- •7. Предел послед. И крит. Коши его существ.
- •8. Существование предела монотонной огран. Послед.
- •9.Предел. Послед. И арифмет. Операц.
- •10.Теорема Больцано-Вейерштарсса.
- •11.Предел функции.
- •12. Бесконечно малые и большие функции.
- •13.Предел ф-ции и арифмет. Операции.
- •14.Предел ф-ции и неравенства.
- •15.Предел. Отнош. Синуса. К. Аргумент.
- •16 .Число е.
- •18. Предел композиции.
- •19.Непрерывность ф-ции в точке.
- •20.Точки разрыва функции.
- •21. Арифметические опер. Над непрерывными ф-циями
- •23.Огранниченность ф-ции непрер. На отрезке.
- •25. Сущ. Наиболь. И наимен. Знач. Ф-ций. Непр.На отрез
- •27. Равномерная непрерывность функций
- •26.Непр. Элементарн.Ф-ций.
- •28.Дифференцируемость функций. Дифференциал и произв.
- •30.Непрерывность ф-ции, имеющей производную.
- •32. Производные элементарных функций.
- •34. Дифференцирование обратной функции.
- •36. Теорема Ферма.
- •37. Теорема Ролля.
- •38. Теорема Лагранжа
- •40.Формула Тейлора. Остаточный член ф форме Пеано
- •41. Остаточный член. Форм.Тейл.По Лагранжу и Коши.
- •43.Признаки постоянства. Возраст. И убыв. Ф-ции.
- •45. Выпуклость функции
- •46. Tочки перегиба
- •48.Интегрирование подстановкой .
- •49.Интегрирование по частям.
- •50.Интегрирование рациональных функций.
- •51.Интегрирование биноминального дифференциала
- •52.Интегрирование некоторых иррациональных функций.
- •54.2 Условия интегрируемости римана.
- •55.Критерий Коши интегрируемости функций.
- •57.Классы интегрируемых функций.
- •60.Интеграл с переменным верхним пределом, его свойства.
- •61. Формула Ньютона-Лейбница.
- •62. Замена переменной в определенном интеграле.
- •63. Интегрирование по частям. Остаточный член формулы Тейлора в интегральной форме.
- •64. Некоторые приложения определённого интеграла.
15.Предел. Отнош. Синуса. К. Аргумент.
Докажем, что
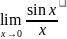 .Так как f(x) =
.Так как f(x) = является четной функцией, то рассмотрим
ее только на интервале (0;
является четной функцией, то рассмотрим
ее только на интервале (0;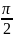 )
Возьмем дугу AM единичного круга,
соответствующую углу, радианная мера
которого равна x. Площадь сектора OAM
заключена между площадями треугольников
OMA и OTA: S
)
Возьмем дугу AM единичного круга,
соответствующую углу, радианная мера
которого равна x. Площадь сектора OAM
заключена между площадями треугольников
OMA и OTA: S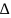 OMA
< Sсек < S4OAT ⇔
OMA
< Sсек < S4OAT ⇔
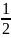 ·
|OA| · |PM| <
·
|OA|2·
x <
·
|OA| · |AT|. Так как |OA| = 1, |MP| = sin x, |AT| = tg x, то
sin
x
< x
< tg
x
⇔
1 <
·
|OA| · |PM| <
·
|OA|2·
x <
·
|OA| · |AT|. Так как |OA| = 1, |MP| = sin x, |AT| = tg x, то
sin
x
< x
< tg
x
⇔
1 <
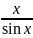 ·<
·<
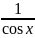 ⇔
cos
x
<
<
1. В силу четности функции cos
x
и
последнее двойное неравенство справедливо
и для интервала ( -
; 0). Таким образом, для любого x ∈(
-
; 0) ∪(0;
) выполняется
неравенство cos
x
<
<
1 Переходя к
пределу при
⇔
cos
x
<
<
1. В силу четности функции cos
x
и
последнее двойное неравенство справедливо
и для интервала ( -
; 0). Таким образом, для любого x ∈(
-
; 0) ∪(0;
) выполняется
неравенство cos
x
<
<
1 Переходя к
пределу при
x → 0 получим 
т.е. =1 – который называют первым замечательным пределом.
16 .Число е.
Пример 1. Доказать справедливость неравенства (неравенство Я. Бернулли)
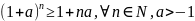
Решение. Докажем, основываясь на методе математической индукции.
1. При n = 1 утверждение, очевидно, справедливо. 2. Предположим, что оно справедливо при n = k, т.е. верно (1 + α) k > 1 + kα.
3.
Докажем, что оно справедливо при n =
k+1.Действительно

![]()
 Согласно
методу математической индукции заключаем,
что утверждение справедливо ∀n
∈
N. Рассмотрим
последовательность {xn},
где
Согласно
методу математической индукции заключаем,
что утверждение справедливо ∀n
∈
N. Рассмотрим
последовательность {xn},
где
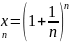 Покажем,
что последовательность {yn},
где
Покажем,
что последовательность {yn},
где
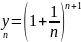 убывающая.
Действительно ∀n
2, находим
убывающая.
Действительно ∀n
2, находим



 Очевидно,
что все члены последова-тельности {yn}
имеют положительные члены, а следова-тельно,
согласно теореме Вейерштрасса, она
имеет предел. Тогда
Очевидно,
что все члены последова-тельности {yn}
имеют положительные члены, а следова-тельно,
согласно теореме Вейерштрасса, она
имеет предел. Тогда 
Определение
1.
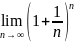 =е
=е
18. Предел композиции.
Теорема
11. Пусть f : X → Y , f(X) = Y , g : Y →
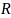 и y0=
,
y0=
и y0=
,
y0=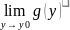 =c
Если существует проколотая окрестность
(x0)
точки x0,
что f(x)
y0
∀x
∈
(x0),
то
=c
Если существует проколотая окрестность
(x0)
точки x0,
что f(x)
y0
∀x
∈
(x0),
то 
доказательство.
Имеем 
Так
как по условию f(x) = y0
в некоторой
(x0),
то 
Так
же имеем

Т огда
в итоге
огда
в итоге
19.Непрерывность ф-ции в точке.
Интуитивное представление о непрерывной функции обычно связывают с такой функцией, график которой — непрерывная линия. Определение 1. Функция f(x) называется непрерывной в точке x0, если для любого заданного числа ε > 0 можно найти такое число δ = δ(ε, x0) > 0, что для всех x, для которых |x − x0| < δ, будет выполняться неравенство |f(x) − f(x0)| < ε, или: ∀ε > 0 ∃δ = δ(ε, x0) > 0 : ∀x |x − x0| < δ ⇒ |f(x) − f(x0)| < ε.
Определение
2. Функция f(x) называется непрерывной в
точке x0
если для любой числовой последовательности
{xn}
такой, что
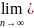 xn=x0
будет
f(xn)
= f(x0).
Так как x − x0
=
x
– приращение аргумента, а f(x) − f(x0)
=
y
– приращение функции в точке x0,
то: Определение 3. Функция f(x)
называется непрерывной в точке x0,
если бесконечно малому приращению
аргумента
x
соответствует бесконечно малое приращение
функции
y,
т.е.
xn=x0
будет
f(xn)
= f(x0).
Так как x − x0
=
x
– приращение аргумента, а f(x) − f(x0)
=
y
– приращение функции в точке x0,
то: Определение 3. Функция f(x)
называется непрерывной в точке x0,
если бесконечно малому приращению
аргумента
x
соответствует бесконечно малое приращение
функции
y,
т.е.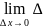 y=
0. В некоторых случаях приходится
пользоваться понятием односторонней
непрерывности. Определение 4. Функция
f(x),
определенная в некоторой левой (правой)
окрестности точки x0
называется непрерывной слева (справа)
в точке x0,
если существует предел слева (справа)
функции y
= f(x)
и он равен f(x0).
Другими словами:
y=
0. В некоторых случаях приходится
пользоваться понятием односторонней
непрерывности. Определение 4. Функция
f(x),
определенная в некоторой левой (правой)
окрестности точки x0
называется непрерывной слева (справа)
в точке x0,
если существует предел слева (справа)
функции y
= f(x)
и он равен f(x0).
Другими словами:
f(x)
непрерывна справа в точке x0
⇒
∃
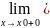 f(x)
= f(x0); f(x)
непрерывна слева в точке x0 ⇒ ∃
f(x)
= f(x0); f(x)
непрерывна слева в точке x0 ⇒ ∃
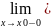 f(x)
= f(x0). Из определения односторонней
непрерывности в точке x0
и свойств предела функции следует:
f(x)
= f(x0). Из определения односторонней
непрерывности в точке x0
и свойств предела функции следует:
Теорема 1. Функция f(x), определенная в некоторой δ-окрестности точки x0, непрерывна в точке x0 тогда и только тогда, когда она непрерывна в этой точке слева и справа.
