6. Лемма о конечном покрытии.

Лемма 4. Из всякой системы интервалов, покрывающей данный отрезок, можно выделить конечную подсистему интервалов, покрывающих этот отрезок. Доказательство. Пусть S = {U} - система интервалов, покрывающая отрезок [a, b] = I₁. Если бы отрезок I₁ не допускал покрытия конечным набором интервалов системы S, то поделив I₁ пополам, мы получили бы, что по крайней мере одна из его половинок, которую мы обозначим через I₂, тоже не допускает конечного покрытия. С отрезком I₂ проделаем ту же процедуру деления пополам, получим отрезок I₃ и т.д. Таким образом, возникает последовательность I₁ ⊃ I₂ ⊃ . . . ⊃ I_n ⊃ . . . вложенных отрезков, не допускающих конечного покрытия интервалами системы S. Поскольку длина отрезка, полученного на n-м шаге, по построению равна |I_n| = |I₁|/2^n-1, то в последовательности {I_n} есть отрезки сколь угодно такой длины. По лемме о вложенных отрезках существует точка C, принадлежащая всем отрезкам I_n, n ∈ N. Поскольку C ∈ I₁ = [a, b], то найдется интервал

(α, β) = U ∈ S системы S, содержащий точку C, т.е α < C < β. Пусть ε = min{C − α, β − C}. Найдем в построенной

последовательности такой отрезок I_n, что |I_n| < ε. Поскольку C ∈ I_n и |I_n| < ε, заключаем, что I_n ⊂ U = (α, β). Но это

противоречит тому, что отрезок I_n нельзя покрыть конечным набором интервалов системы.

7. Предел послед. И крит. Коши его существ.

Определение 2. Число a называется пределом числовой последовательности {x_n}, если для любого сколь угодно малого положительного числа ε найдется такое натуральное число n₀ = n₀(ε), что для всех 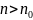выполняется

Неравенство

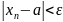
В этом случае говорят, что последовательность имеет предел и пишу

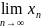
можно записать более кратко:

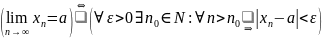
Последовательности, имеющие предел 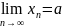называют сходящимися (к числу a), а последовательности, не имеющие конечного предела - расходящимися.Понятие предела последовательности связано в определенном смысле с встречающейся на практике задачей получения значения некоторой интересующей нас величины с наперед заданной фиксированной точностью ε > 0. Последовательные приближенные значения x_n, рассматриваемой величины могут получаться в результате проведения каких-либо экспериментов, или вычисления по каким-нибудь рекуррентным формулам или каким-то другим путем. Эта задача будет, очевидно, решена, если найдется номер n₀, начиная с которого все значения x_n будут отклоняться от точного значения a рассматриваемой величины в пределах заданной точности. Конечно, если указанное n₀ существует лишь для одного данного ε > 0, это еще не означает, что последовательность {x_n} сходится: в определении предела последовательности требуется, чтобы соответствующий номер n₀ можно было бы подобрать для любого ε > 0. Так как {|x_n − a| < ε} = V (a, ε), то из определения предела следует, что если число a является пределом последовательности {x_n}, то в произвольную сколь угодно малую ε-окрестность точки попадают все члены этой последовательности, начиная с некоторого n > n₀ ∈ N. Крит.Коши: Определение 1. Последовательность {x_n} называется фундаментальной (или последовательностью Коши), если для любого числа ε > 0 найдется такой номер N ∈ N, что из n > N и m > N следует |x_n − x_m| < ε. Теорема 4 (критерий Коши сходимости последовательности). Числовая последовательность сходится тогда и только тогда, когда она фундаментальна. Док-во. Необходимость. 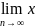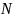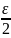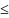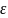Пусть _n=a Тогда, согласно определения, ε > 0 ∃N ∈ : ∀l > N ⇒ |x_l − a| < Если теперь m > N и n > N, то |x_m − x_n| = |x_m − a + a − x_n| |x_m − a| + |x_n − a| < + = т.е. сходящаяся последовательность фундаментальна.