60.Интеграл с переменным верхним пределом, его свойства.

Пусть f ∈ R[a; b]. Тогда согласно лемме 1 она интегрируема на любом отрезке [a; x] ⊂ [a; b]. Рассмотрим функцию

Эта функция называется интегралом с переменным верхним пределом.

Теорема 17. Если f∈R[a;b], то при любом x∈[a;b] определена функция 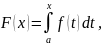(3.20) и F(x) ∈ C[a; b].

Доказательство. Существование интеграла (3.20) при любом x ∈ [a; b] следует из леммы 1, поэтому остается проверить

непрерывность функции F(x). Поскольку f∈C[a;b], то|f(x)|≤M<∞ на [a; b]. Пусть x ∈ [a; b] и x+h ∈ [a; b]. Тогда в силу аддитивности интеграла получаем

Отсюда следует, что lim _h→0|4F(x)| = 0, а это и означает, что функция (3.20) непрерывна в каждой точке x ∈ [a; b].

Теорема 18. Если f ∈ R[a; b] и функция f(x) непрерывна в некоторой точке x ∈ [a; b], то функция F(x), определенная

на [a; b] формулой (3.20), дифференцируема в этой точке x, причем имеет место равенство F’(x) = f(x).

Доказательство. Пусть x ∈ [a; b], x + h ∈ [a; b]. Оценим

Так как f(x) непрерывна в точке x, то

∀ε>0 ∃δ>0: ∀t∈[a;b] |t−x|<δ⇒|f(t)−f(x)|< ε.

Пусть |h| < δ. Тогда

Отметим, что если x = a или x = b, то под F(x) понимаем соответствующие односторонние производные.

Теорема 19. Каждая непрерывная на отрезке [a; b] функция f(x) имеет на этом отрезке первообразную, причем

любая первообразная функции f(x) на [a; b] имеет вид

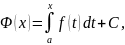(3.21)

где C - некоторая постоянная.

Доказательство. Поскольку f ∈ C[a; b], то f ∈ R[a; b], поэтому, на основании теоремы 18, функция (3.20) является

первообразной для f(x) на [a; b]. Но две первообразные Φ(x) и F(x) одной и той же функции на отрезке могут отличаться

на этом отрезке только на постоянную, поэтому Φ(x) = F(x) + C.

61. Формула Ньютона-Лейбница.

Теорема 20 (основная теорема интегрального исчисления). Если f ∈ C[a;b] и Φ(x) любая первообразная функции f(x) на [a; b], то

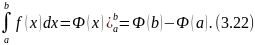
Доказательство. Из условия следует, что функция f(x) имеет первообразную. Все множество первообразных дается формулой 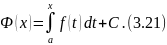Значит имеем

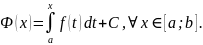
Полагая x = a, получим C = Φ(a), откуда

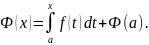
Полагая в последнем выражении x = b, получим формулу совпадающую с (3.22) с точностью до обозначения переменной интегрирования. Формула (3.22) называется формулой Ньютона-Лейбница.

Для дальнейших приложений расширим понятие первообразной.

Определение 1. Непрерывная на числовом промежутке функция Φ(x) называется первообразной (обобщенной первообразной) функции f(x), определенной на том же промежутке, если во всех точках промежутка, за исключением, может быть, конечного их числа, имеет место соотношение Ф’(x)=f(x).

Теорема 19’. Каждая определенная и ограниченная на отрезке [a;b] функция f(x) с конечным множеством точек разрыва имеет на этом отрезке (обобщенную) первообразную, причем любая первообразная функции f(x) на [a;b] имеет вид (3.21).

Доказательство. Поскольку f(x) имеет конечное множество точек разрыва, то f∈R[a;b] и, следовательно, функция F(x) является обобщенной первообразной для f(x) на [a;b]. При этом заметим, что F(x) непрерывна на [a;b]. Если Φ(x) другая первообразная функции F(x) на [a; b], то Φ(x) − F(x) - непрерывная функция, постоянная на каждом из конечного числа промежутков, на которые точки разрыва функции f(x) разбивают отрезок [a; b]. Из непрерывности Φ(x) − F(x) на [a;b] тогда следует, что Φ(x) −F(x) ≡ const на [a;b].

Теорема 20’. Если f : [a; b] → R - ограниченная функция с конечным числом точек разрыва, то f ∈ R[a; b] и

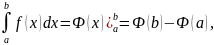
где Φ(x) -любая из первообразных функции f(x) на отрезке [a;b].