30.Непрерывность ф-ции, имеющей производную.

Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке. Доказательство. Пусть функция f(x) дифференцируема в точке x₀, т.е y = A · x + o( x), x → 0. 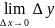= A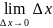 + 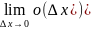= 0, что и означает непрерывность функции f(x) в точке x₀.

Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке. Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.

31. Правила вычисления производных. Теорема 3. Если функции f : X → R, g : X → R дифференцируемы в точке x ∈ X, то а) их сумма дифференцируема в x, причем (f + g)’(x) = (f’+ g’)(x); б) их произведение дифференцируемо в x, причем (f · g)’(x) = f’(x)g(x) + f(x)g’(x); в) их отношение дифференцируемо в x, если g(x) 0, причем( 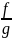) ‘(x) =

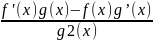
Следствие 1. Производная от линейной комбинации дифференцируемых функций равна линейной комбинации производных этих функций. Следствие 2. Если функции f₁(x), f₂(x), . . . , f_n(x) дифференцируемы в точке x, то. (f₁ · f₂ · . . . · f_n)’(x) = f’₁(x) · f₂(x) · . . . · f_n(x) + f₁(x) · f’₂(x) · . . . · f_n(x) + . . . + f₁(x) · f₂(x) · . . . · f’_n(x).

Следствие 3.Из взаимосвязи производной и дифференциала следует, что теорема 3 может быть записана также через дифференциалы, т.е. а) d(f + g)(x) = df(x) + dg(x), в) d(f · g)(x) = g(x) · df(x) + f(x) · dg(x); с) d( ) (x) =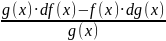 , если g(x) = 0.

32. Производные элементарных функций.

а). Производная и дифференциал логарифмической функции. Пусть y = log _a x, где a > 0,a 1. Тогда y = log a (x + x) – log _a x = log _a(1 +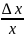 ). Следовательно, по определению y₀=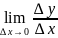 = =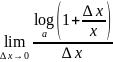 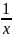log_a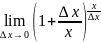 = log_a e=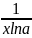 . Здесь воспользовались вторым замечательным пределом и непрерывностью логарифмической функции. Итак, y = log_a x ⇒ y₀= log_a e= ⇒ dy =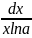 . б). Производная и дифференциал степенной функции Пусть y =(u(x))^α, α ∈ R. Рассмотрим вначале случай, когда u(x) > 0. Если u(x) > 0, то ln y = α ln u(x). Продифференцируем полученное равенство почленно по правилу дифференцирования сложной функции, считая y функцией от x: (ln y)’ = (α ln u(x))’ ⇒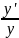 = 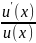⇒ dy = . 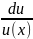Пусть теперь u(x) < 0. Представим функцию y = (u(x)) ^α в виде (−1)^α (v(x)) ^α , где v(x) > 0. Тогда y’= (−1)^αα(v(x))^α−1v’(x) = α(u(x))^α−1u’(x). Итак y =(u(x))^α

⇒ y’= α(u(x))^α−1u’(x) ⇒ dy = α(u(x))^α−1du(x).

33Дифферен. И производн. Композиц. Ф-ции. Теорема 4. Если функция f : X → Y ⊂ R дифференцируема в точке x, а функция g : Y → R дифференцируема в точке y = f(x) ∈ Y , то композиция g ◦ f : X → R этих функций дифференцируема в точке x, причем (g ◦ f)’(x) = g’(f) · f ’(x). Доказательство. Условия дифференцируемости функций f и g имеют вид f(x + h) − f(x) = f ‘(x)h + o(h), h → 0, x + h ∈ X, g(y + t) − g(y) = g’(y)t + o(t), t → 0, y + t ∈ Y. Заметим, что в силу последнего равенства функцию o(t) можно считать определенной и при t = 0, а в представлении o(t) = γ(t) · t, где γ(t) → 0 при t → 0, y + t ∈ Y , можно считать γ(0) = 0. Полагая f(x) = y, f(x + h) = y + t в силу дифференцируемости, а значит, и непрерывности функции f в точке x заключаем, что при h → 0 также t → 0, и если x + h ∈ X, то y + t ∈ Y . По теореме о пределе композиции теперь имеем γ (f(x + h) − f(x)) = α(h) → 0, h → 0, x + h ∈ X и, таким образом, т.к. t = f(x + h) − f(x), то o(t) = γ(f(x + h) − f(x))(f(x + h) −f(x))= α(h)(f ’(x)h + o(h))= α(h)f’(x)h + α(h)o(h) = o(h) + o(h) = o(h), h → 0, x + h ∈ X. Далее (g◦f)(x+h)−(g◦f)(x) = g(f(x+h))−g(f(x))= g(y+t)−g(y) = g‘(y)t+o(t) = g‘(y)(f(x+h)−f(x))+o(f(x+h)−f(x))= g’(y)(f’(x)h + o(h))+o(f(x + h) − f(x))= g’(y)f ’(x)h + g’(y)o(h) + o(f(x+h) − f(x)). Заметим, что сумма g’(y)o(h) + o(f(x + h) − f(x)) есть величина бесконечно малая в сравнении с h при h → 0,x + h ∈ X т.к. o(f(x + h) − f(x))= o(h), h → 0, x + h ∈ X. В итоге (g ◦ f)(x + h) − (g ◦ f)(x) = g’(f) · f’(x)h + o(h), h → 0, x + h ∈ X.