25. Сущ. Наиболь. И наимен. Знач. Ф-ций. Непр.На отрез

Т еорема 5 (Больцано-Коши). Если функция f(x) непрерывна на отрезке [a; b] и f(a) = A, f(b) = B, то для любого C, заключенного между A и B, существует такая точка ξ ∈ [a; b], что f(ξ) = C. Доказательство. Пусть для определенности f(a) = A < B = f(b) и A < C < B. Разделим отрезок [a; b] точкой x0 на два равных по длине отрезка; тогда либо f(x₀) = C и, значит, искомая точка ξ = x₀ найдена, либо f(x₀) C и тогда на концах одного из полученных отрезков функция f(x) принимает значения, лежащие по разные стороны от числа C, точнее - на левом конце значение меньшее C, на правом - большее. Обозначим этот отрезок [a₁; b₁] и разделим его снова на два равных по длине отрезка и т.д. В результате либо через конечное число шагов придем к искомой точке ξ, в которой f(ξ) = C, либо получим последовательность вложенных отрезков [a_n, b_n], по длине стремящихся к нулю и таких, что f(a_n) < C < f(b_n). (1) Пусть ξ - общая точка всех отрезков [an; bn], n = 1, 2, . . . Как известно ξ = 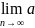_n = b_n . 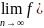Поэтому, в силу непрерывности функции можем записать f(ξ) = _n) =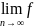 (b_n) Тогда из (1) _n) C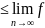 (b_n). т.е. f(ξ) = C. Следствие 1. Если функция непрерывна на отрезке и на его концах принимает значения разного знака, то на этом отрезке существует хотя бы одна точка, в которой функция обращается в нуль. Следствие 2. Пусть функция f(x) непрерывна на отрезке [a; b] и M = Тогда функция f(x)

п ринимает все значения из отрезка [m;M] и только эти значения. Доказательство. Заметим, что если

то m f(x) M, и согласно теореме 4, существуют такие точки α ∈ [a; b] и β ∈ [a; b], что f(α) = m, f(β) = M. Следовательно, следствие 2 непосредственно вытекает из теоремы 5, примененной к отрезку [α; β], если α β, или, соответственно, к отрезку [β; α], если β < α. Таким образом, множество всех значений функции, заданной и непрерывной на некотором отрезке, представляет собой также отрезок.

27. Равномерная непрерывность функций

О пределение 1. Функция f(x) называется равномерно-непрерывной на множестве X ⊂ R, если для любого ε > 0 найдется δ = δ(ε) > 0, такое, что для любых x₁, x₂ ∈ X, удовлетворяющих условию |x₁−x₂| < δ, выполняется неравенство |f(x₁) − f(x₂)| < ε. Если f(x) равномерно-непрерывна на множестве X, то она непрерывна на множестве X. Чтобы в этом убедиться, достаточно положить x₁ = x, x₂ = x₀. Тогда из определения равномерной непрерывности функции следует определение непрерывной функции в точке x₀. Обратное утверждение не всегда справедливо. Теорема 8 (Кантора). Функция, непрерывная на отрезке, равномерно непрерывна на этом отрезке. Доказательство. Пусть f : X → R, и f ∈ C([a; b]), где X = [a; b]. Поскольку f(x) непрерывна в любой точке x ∈ X, то по ε > 0 можно найти такую δ-окрестность V_δ(x) точки x, что колебание ω(f, V_δ(x)), где

функции f(x) окажется меньше ε. Для каждой точки x ∈ X построим окрестность V_δ(x) обладающую этим свойством. Величина δ при этом может меняться от точки к точке, т.е. δ = δ(x). Интервалы V_δ/2(x), x ∈ X в совокупности образуют покрытие отрезка X = [a; b], из которого по лемме о конечном покрытии можно выделить конечное подпокрытие V_δ/2(x1), . . . , V_δ/2(xn). Пусть δ = min{ δ(x₁), . . . , δ(x_n)}. Покажем, что для любых точек x’

, x’’∈ X таких, что |x’− x’’| < δ выполнено|f(x’) − f(x’’)| < ε. Действительно, поскольку система интервалов V_δ/2(x₁), . . . , V_δ/2(x_n) покрывает X, то найдется интервал V_δ/2(x_i) этой системы, который содержит точку x’ т.е. |x’− x_i| < δ(x_i). Но в таком случае |x’’− x_i| |x’− x’’| + |x’− x_i| < δ + δ(x_i) < δ(x_i) + δ(x_i) = δ(x_i). Следовательно x’, x’’∈ V_δ(xi)(x_i) и потому |f(x’) − f(x’’)| ω(f, V_δ(xi)(x_i))< ε.