7. Исследование знакополож.Рядов. Признак Даламбера и Коши.

Знакоположительный ряд-ряд, все слагаемые которого- положительные числа.

Сумма а n-e знакоположительн. n-е >0/

Критерии сходимости знакополож.рядов:

Чтобы знакополож.ряд сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. ( -последовательность его частичных сумм)

Доказательство:

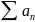знакоположительн ряд, значит -возрастает.

Необходимость:

По условию ряд -сходится, т.е.

и возрастает, тогда частичная сумма с предельной суммы ряда

Последовательность

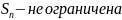
Достаточность:

1. По условию

2. Последовательность частичных сумм возрастает.

Если последовательность возрастает и ограничена сверху, то по теореме Вейерштрасса она сходится, имеет предел.

Примечание: Достаточные признаки сходимости знакоположит.рядов являются следствием этого критерия.

ПРИЗНАК ДАЛАМБЕРА

Если для знакоположит.ряда существует предел отношения 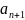к , тогда при d<0 ряд сходится, а при d>0-расходится.

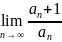= d

Примечания: 1.При d=1 признак ответа не даети для исследования ряда надо применять другой признак сходимости.

2. из 1-го следует =g

Пример применения

-?

=

= =

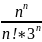
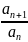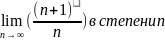d=lim = Lim =1/3 =1/3 = 1/3 =1/3*e=e/3

ПРИЗНАК КОШИ

Если для знакоположит.ряда существует предел 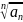=k, при к<1, ряд сходится, при к>1-расходится. При к=1-признак ответа не дает.

Примечание: ряд вида =

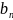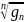= =g

Пример применения:

=

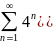
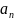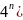
lim =lim -вся формула под корнем= =

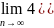4 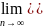= 4*е>1-расходится.

8. Интегральный признак сходимости знакоположительных рядов. Условие сходимости обобщенного гармонического ряда.

Интегральный признак

Пусть дан ряд ∑ f(n)= =f(1)+f(2)+f(3)+… слагаемые кот. явл. значением некоторой функции y=f(x) положительно непрерывны и убывающ. На интервале [1;+∞), тогда если ∫ f(x)dx=k прин.R то∑ f(n)сход.=числу, если ∫ f(x)dx=∞, то ∑ f(n) расх.=∞

Пр. ∑ 1/n² - ? заменяем n²-x²

1)y=1/x² на [1;+∞) на 0 : нельзя полож.. непрерыв., убывающ. →использ.интегр.призн.

2) ∫ dx/x² = ∫x^-2dx=lim ∫x^-2dx=lim (x^-2+1/_-2+1|^b₁)= lim(-x^-1|^b₁)=lim(-¹/_x|^b₁)=lim(-¹/_b+1=1 шпора на полях ∫xⁿdx=xⁿ⁺¹/n+1 +С при n≠-1 ∫dx/x=ln|x|+C

∫f(x)dx=F(b)-F(a)

вывод: несобственный интеграл сходится, значит ∑ 1/n²сх. по интегр. признаку(выражение вида∫f(x)dx наз-ся несобственным интегралом).

Условие сходимости обобщенного гармонического ряда.

ОГР наз-ся ряд вида ∑ 1/n^α,α прин. (действит.число) с помощью интегрального признака можно док-ть, что ОГР сходится при α>1, расход.α≤1

9. Знакопеременные числовые ряды. Абсолютная и условная сходимость знакопеременного ряда.

Числовой ряд содержащий бесконечное множество отрицательных и бесконечное множество положительных членов называется знакопеременной.

Пр: 1-1/2+1/3-1/4-1/5+1/6-1/7-1/8-1/9+1/10 – знакочеред.

Частным случае знакопеременного ряда, т.е ряд в котором последоват.члены имеют противоположные снаки.

ПР: 1-1/2+1/3-1/4+1/5-1/6+1/4-1/8+….

Ряд ∑аn называется знакочередующим, если для любого номера произведение двух соседних слогаемых<0.

Примечание: Свойство числовых рядов (бесконечных сумм)могут отличаться от свойств конечных сумм.

Пр:

Переставим и сгруппируем слагаемые этого ряда

=(1-1/2-1/4)+(1/3-1/6-1/8)+(1/5-1/10-1/12)+…-

В каждой скобке выполнили только 1 вычит.

1/2-1/4+1/6-1/8+1/10-1/12+…=1/2(1-1/2+1/3-1/4+1/5-1/6+1/7-1/8+..)+..

Парадокс: при перестановки слагаемых сумма ряда уменьшилась в двое.

Теорема Лейбница. (достаточный признак сходимости знакочеред.ряда)

Если члены знакочеред.ряда убывают по абсолютной велич и стремятся к 0, то ряд сходится

∑ аn n аn* аn+1<0

Сход n |аn+1|< |аn| (знаки черед.)

Ряды удовлетворяют условие теор. Лейбница и назыв.рядами лейбница (всегда сходятся)

Пр:1-1/2+1/3-1/4+1/5-1/6+1/7 – ряд. Лейбн.

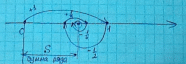
Рассмотрим частичн. суммы данного ряда мы получим посл. стягивающихся отрезков, длины которых стремятся к бесконечности. Эти отрезки имеют единственную общую точку, координаты этой точки и будет значением суммы ряда (S)

Абсолютная и условная сходимость знака переменных рядов.

Числовой ряд сходится абсолютно, если сходится ряд составленный из модулей его членов.

Пр:

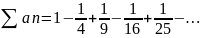
α=1→cходится

ОГР сходится α>1

Расходится α<=1

Вывод:

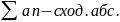
Числовой ряд сходится условно, если он сходится, но не абсолютно, т.е

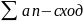усл, если 1)

2) : - расходится.

Приме:

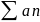= 1-1/2+1/3-1/4+1/5- сходится, т.к. ряд Лейбница

=1+1/2+1/3+1/4+1/5=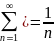 - расходится

Вывод: = сходится, т.к. ряд Лейбница

-расходится, т.к.гармонический рядю, следовательно –сход.условно

Примечание: Ряд Лейбница могут сходится как условно, так и абсолютно,т.е. признак Лейбница не позволяет определить характер сходимости.

Свойства абсолютн.сходимости рядов.

1. Если ряд сходится абсолютно, то он сходится . Сходится , то сходится.

2. При любой перестановке слагаемых сумма абсолютной сходимости ряда не меняется.

3. Если ряд сходится абсолютно и сходится к числу А, то ряд (R* ), так же сходится абсолютно и сходится к числу R*A, R€R

4. Eсли и сходятся абсолютно, причем сходится к A, cходится к B, то 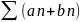следовательно будет сходимость абсолютная и сходится к А+В.

5. Eсли и сходятся абсолютно, причем сходится к A, cходится к B, то ряд составленный из всевозм. произведений 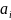* 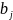, где i=1;2.. j=1;7…

также сходится абсолютно, причем сходится к числу A*B.