20 Понятие функции действительного переменного. Способы задания функции.

Если каждому значению переменной х из множества {x} ставится в соответствие по известному закону некоторое число у, то говорят, что на множестве {x} задана функция y=y(x) или y=f(x). При этом переменная х называется аргументом, а множество {x} – областью задания функции y=f(x). Число у, которое соответствует данному значению аргумента х, называется частным значением функции в точке х. Совокупность всех частных значений функции образует вполне определенное множество {y}, называемое множеством всех значений функции. В обозначении y=f(x) буква f называется характеристикой функции. Способы задания функции. Часто закон, устанавливающий связь между аргументом и функцией, задается с помощью формул. Такой способ задания функции называется аналитическим. Следует подчеркнуть, что ф-ция может определяться разными формулами на разных участках области своего задания. Довольно распространенным способом задания функции является табличный способ, заключающийся в задании таблицы отдельных значений аргумента и соответствующих им значений ф-ции. Также используется способ интерполяции, заключающийся в замене ф-ции между ее табличными значениями какой-либо простой функцией. Примером табличного задания функции может служить расписание движения поезда. Интерполяция позволяет приближенно определить местоположение поезда в любой промежуточный момент времени. В практике физических измерений используется и еще один способ задания ф-ции – графический, при котором соответствие между аргументом и функцией задается посредством графика.

21 Два определения предела в точке (по Гейне и Коши), их эквивалентность.

Опр1 (Гейне) Число b называется предельно малым числом функции y=f(x) в точке а, если (1) Замечание1 Если есть предельное значение b, то оно единственное. Замечание2 Предельное значение для кратности называют пределом и обозначают (2) Опр2(Коши) Число b= , если a>0 для х . (3) Замечание3 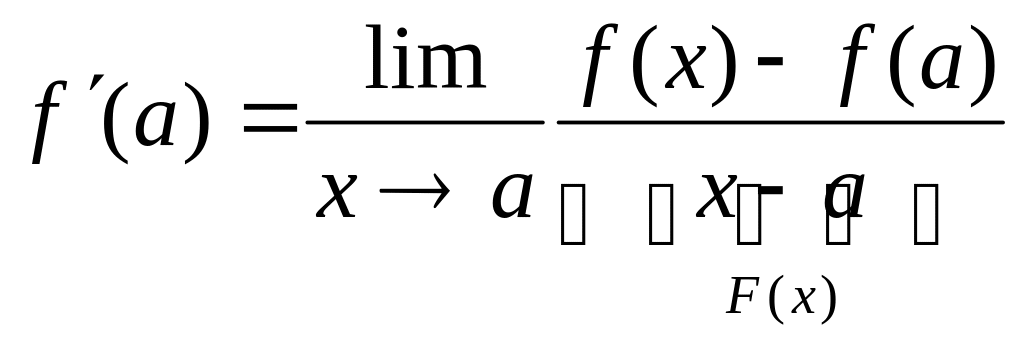Теорема. Определение предела по Гейне и по Коши эквивалентны. Док-во: 1)Из Коши вытекает Гейне. Пусть >0 существует . 0<|x-a|< выполняется нер-во . для существует 0< существует . 2) Из Гейне вытекает Коши: Пусть Гейне выполняется, но на самом деле нет = противоречие. Док-во: Существует существует . ; , , но .

22 Критерий Коши существования предела функции.

Теорема Для того, чтобы функция имела в точке а предел необходимо и достаточно: для любого >0 существовал и для любого и (1) Док-во: 1)Необходимость ; для любого >0 и , что при выполняется нер-во . . 2)Достаточность: для любого существует . Р=1,2,…, . . 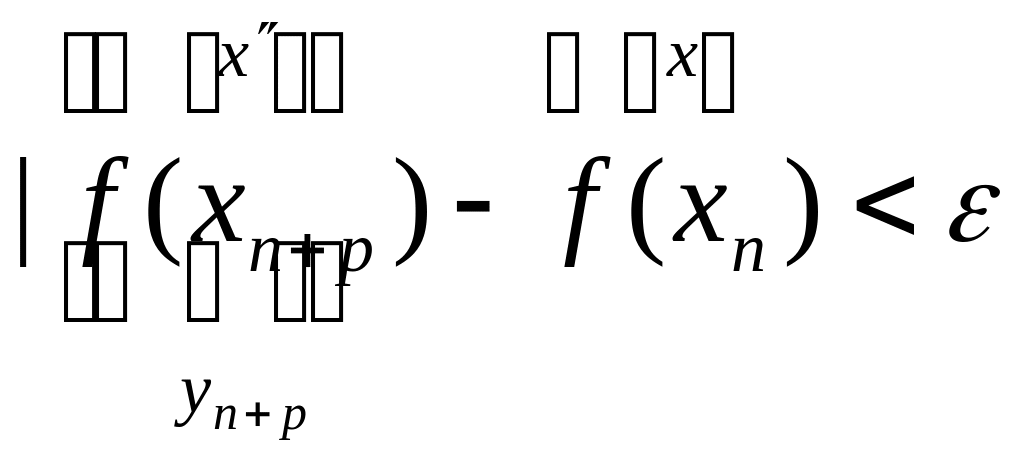фундаментальная, поэтому сходится и .

23 Арифметические операции над функциями, имеющими предел в данной точке.

Теорема Пусть заданные на одном и том же множестве функции f(x) и g(x) имеют в точке а предельные значения b и с. Тогда ф-ции f(x)+g(x), f(x)-g(x), f(x)*g(x) и f(x)/g(x) имеют в точке а предельные значения (частное при условии с 0), равные соответственно b+c, b-c, b*c и b/c. Док-во: Пусть - произвольная сходящаяся к а посл-ть значений аргумента функций f(x) и g(x). Соответствующие посл-ти и значений этих ф-ций имеют пределы b и с. Но тогда посл-ти и имеют пределы соотв-но равные b+c, b-c, b*c и b/c. В силу произвольности посл-ти { } это означает, что Теорема доказана. Имеет место следующее утверждение: в каждой точке а бесконечной прямой предельные значения многочленов и несократимых алгебраических дробей существуют и равны частным значениям этих ф-ций в указанной точке. Действительно, в силу вышедоказанной теоремы = Аналогично можно убедиться, что Следовательно, для многочлена получим =