Распределение Максвелла

М олекулы газа вследствие теплового движения испытывают многочисленные соударения друг с другом. При каждом соударении скорости молекул изменяются как по величине, так и по направлению. В результате в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям, зависящее от абсолютной температуры Т. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а величины скоростей подчиняются определенной закономерности. Распределение молекул газа по величине скоростей называется распределением Максвелла.

Если одновременно измерить скорости большого числа N молекул газа и выделить некоторый малый интервал скоростей от v до v+ v, то в выделенный интервал  v попадает некоторое число  N молекул. На графике удобно изображать зависимость величины   от скорости v. При достаточно большом числе N эта зависимость изображается плавной кривой, имеющей максимум при   (наиболее вероятная скорость). Здесь m - масса молекулы,  - постоянная Больцмана.

Характерным параметром распределения Максвелла является так называемая среднеквадратичная скорость   означает среднее значение квадрата скорости. В молекулярной физике доказывается, что

где  - молярная масса.

Из выражения для среднеквадратичной скорости следует, что средняя кинетическая энергия поступательного движения молекул газа есть

Распределение Максвелла является одной из важнейших статистических закономерностей молекулярной физики.

Билет №34.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения   одинаково), барометрическая формула имеет следующий вид:

где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне ( ),   — молярная масса газа,   — газовая постоянная,   — абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону:

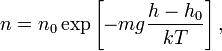
где   — масса молекулы газа,   — постоянная Больцмана.

Распределение Больцмана.

ри выводе основного уравнения МКТ предполагалось, что на молекулы не действуют внешние силы, и поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул – с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул и давление газа убывают с высотой.

Если температура воздуха T и ускорение свободного падения g не меняются с высотой, то давление воздуха p на высоте h, отсчитанной от некоторого уровня, принятого за начальный, связано с давлением p₀ на этом начальном уровне экспоненциальной зависимостью:

p(h)=p₀e^(-Mgh/RT) (36)

Выражение (36) называется распределением Больцмана, или барометрической формулой. Оно позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту.

Из формулы (36) сле¬дует, что давление убывает с высотой тем быстрее, чем тяжелее газ (чем больше его молярная масса M) и чем ниже температура T.

Барометрическую формулу (36) можно преобразовать, воспользовавшись выражением (19):

n(h)=n₀e^(-Mgh/RT), (37)

Где n – концентрация молекул на высоте h, n₀ – концентрация молекул на высоте h=0. Так как M=m₀N_A и k=R/N_A, то:

n(h)=n₀e^(-m₀^{gh/kT), (38)}

гдеm₀gh - потенциальная энергия одной молекулы в поле тяготения, и:

n(h)=n₀e^{(-П/kT). (39)}

Выражение (39) называют законом Больцмана для распределения частиц во внешнем потенциальном поле. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Б илет № 35.

Длина свободного пробега молекулы — это среднее расстояние (обозначаемое  ), которое частица пролетает за время свободного пробега от одного столкновения до следующего.

Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега (<λ>). Величина <λ> является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.

, где   — эффективное сечение молекулы,   — концентрация молекул.

В термодинамически неравновесных системах происходят особые необратимые процессы, называемые явлениями переноса, в результате которых осуществляется пространственный перенос массы, импульса, энергии. К явлениям переноса относятсятеплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса). Ограничимся одномерными явлениями переноса. Систему отсчета будем выберать так, чтобы ось х была направлена в сторону в направления переноса. 

3. Внутреннее трение (вязкость). Суть механизма возникновения внутреннего трения между параллельными слоями газа (жидкости), которые движущутся с различными скоростями, есть в том, что из-за хаотического теплового движения осуществляется обмен молекулами между слоями, в результате чего импульс слоя, который движется быстрее, уменьшается, который движется медленнее — увеличивается, что приводит к торможению слоя, который движется быстрее, и ускорению слоя, который движется медленнее.  Как известно, сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:   (5)  где η — динамическая вязкость (вязкость), dν/dx — градиент скорости, который показывает быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F.  Согласно второму закону Ньютона взаимодействие двух слоев можно рассматривать как процесс, при котором в единицу времени от одного слоя к другому передается импульс, который по модулю равен действующей силе. Тогда выражение (5) можно записать в виде   (6)  где j_p — плотность потока импульса — величина, которая определяется определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, dν/dx — градиент скорости. Знак минус говорит о том, что импульс переносится в направлении убывания скорости (поэтому знаки j_p и dν/dx противоположны).  Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле   (7)  Из сопосавления формул (1), (3) и (6), которые описывают явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были известны еще задолго до того, как они были обоснованы и получены из молекулярно-кинетической теории, которая позволила установить, что внешнее сходство их математических выражений является следствием общностью лежащего в основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.  Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетической сути коэффициентов λ, D и η. Выражения для коэффициентов переноса получаются из кинетической теории. Они записаны без вывода, поскольку строгое и формальное рассмотрение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (2), (4) и (7) дают связь коэффициентов переноса и характеристики теплового движения молекул. Из этих формул следуют простые зависимости между λ, D и η:  и   

Билет №36.