Примеры расчета момента инерции.

1. Стержень

2. Кольцо (тонкостенный цилиндр).

3. Диск (сплошной цилиндр).

=

4. Толстостенный цилиндр.

5. Сферическая оболочка. (В декартовый координатах).

+ =

+ =

=

= =

6. Шар.

Билет №11.

Изменение механического движения тела и, следовательно, его механической энергии происходит в процессе механического действия на рассматриваемое тело со стороны других тел. Мерой этого действия служат соответствующие силы. Поэтому следует говорить об изменении механической энергии тела под влиянием приложенных к нему сил. Для количественного описания такого процесса изменения энергии тела вводят в механике понятие работы силы.

Элементарной работой силы на малом перемещении точки приложения силы называется скалярное произведение на : =

где и - радиус-вектор и скорость точки , - малый промежуток времени в течение которого сила совершает работу .

Так как скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, то

=

где - путь точки за малое время , -угол между силой и элементарным перемещением (или скоростью ) точки , - проекция силы на направление (или ).

Сила не совершает работы в двух случаях:

1). Точка приложения силы неподвижна ( =const, а =0)

2). Угол , то есть сила направлена по нормали к траектории точки ее приложения. .

Если угол острый, то сила движущая, если тупой, то тормозящая.

Согласно правилу скалярного умножения векторов, элементарная работа силы в декартовых координатах равна: =

Работа, совершаемая силой на конечном перемещении точки ее приложения из положения 1 в положение 2

равна сумме элементарных работ силы на всех малых участках траектории от точки 1 до точки 2. Эта сумма п риводится к интегральной: .

Работа при прямолинейном движении равна: и численно равна площади под графиком.

Р абота потенциальной силы на произвольной замкнутой траектории точки ее приложения равна нулю.

1.Если на тело действует постоянная сила F (Рисунок 13), и это приводит к перемещению ∆ r тела, тоэлементарной работой ∆А постоянной силы называется скалярное произведение вектора силы Fи вектора перемещения ∆r: ∆А = (F∙∆r) = ½ F½½∆ r½ cos a ,

где a - угол между направлениями векторов силы F и перемещения ∆r, ( F∙ ∆r) – скалярное произведение двух векторов (см.[8]).

Рисунок 13 - Перемещение тела под действием постоянной силы.

Работа ∆А - скаляр. Если угол a - острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол a - тупой, то ∆А - отрицательная величина, и говорят, что работа совершается против действия силы. Если a = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 90⁰), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.

На рисунке 14 представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F _i и ∆ r _i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F _i на своем малом участке (Рисунок 14): А = ∆А₁ + ∆А₂ +....+ ∆А _N = ( F₁∙∆ r₁) + (F ₂∙∆ r₂) + ...+( F _N∙∆ r_N) =   ( F_i∙∆ r_i),

где i = 1,2...... N - номер элементарного участка траектории. Рисунок 14 - График зависимости силы от пути. На участке ∆r _i силу F_i можно считать постоянной, тогда элементарная работа ∆А_i на участке ∆r _iравна ∆А_i= F_i∙∆ r _i и равна площади заштрихованной фигуры на рисунке 14.

А= ∆А_i - это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.

Работа равнодействующей силы на каком-то участке пути равна алгебраической сумме работ сил составляющих на том оке участке пути.

Билет №12.

Кинетическая энергия.

Кинетической энергией механической системы называется энергия механического движения этой системы. Изменение кинетической энергии материальной точки происходит под действием приложенной к ней силы и равно работе, совершаемой этой силой.

или .

,

Изменение кинетической энергии тела равно работе сил, приложенных к этому телу.

.

Кинетическая энергия механической системы равна сумме кинетических энергий всех частей этой системы. Например, кинетическая энергия системы из n материальных точек равна

где скорость i-й материальной точки, ее масса.

Кинетическая энергия системы полностью определяется значениями масс и скоро­стей входящих в нее материальных точек. Она не зависит от «предыстории» системы, т. е. от того, каким образом части системы приобрели данные значения скоростей. Кратко это важное утверждение формулируют следующим образом: кинетическая энергия системы есть функция состояния ее механического движения. В отличие от импульса кинетическая энергия системы не зависит от того, в каких направлениях движутся ее части.

Кинетическая энергия твердого тела при поступательном движении записывается так же, как и для материальной точки.

Кинетическая энергия вращающегося тела.

Представим энергию всего тела, как сумму энергий материальных точек.

Теорема Кенига:

Значения скорости и кинетической энергии одной и той же материальной точки различны в двух системах отсчета, движущихся друг относительно друга. Рассмотрим 2 системы отсчета: инерциальную систему и систему, движущуюся относительно первой системы со скоростью :

и

- Теорема Кёнига.

Формулировка:«Кинетическая энергия механической системы равна сумме кинетической энергии той же системы в ее движении относительно системы центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью центра масс»

 При сложном движении твердого тела его кинетическая энергия может быть представлена в виде суммы кинетических энергий поступательного и вращательного движений.

Это относится и к плоскому движению твердого тела. Для вычисления кинетической энергии тела при плоском движении удобно пользоваться формулойT =  . (4.9)

Здесь М – масса твердого тела, Vc – скорость его центра масс, Ic – момент инерции относительно оси, проходящей через центр масс, и  – угловая скорость вращения. Очень важно помнить, что эта формула справедлива только тогда, когда ось вращения проходит через центр масс тела.

Билет №13.

Закон изменения кинетической энергии.

Изменение кинетической энергии равно сумме работ, совершаемых при этом всеми внешними и внутренними силами:

,

причем сумму элементарных работ всех сил, приложенных к материальной точке системы удобно разбить на две части:

.

Теорема об изменении кинетической энергии доказанная для точки (§ 14.4) будет справедлива для любой точки системы

Составляя такие уравнения для всех точек системы и складывая их почленно получаем:

или, согласно (19.1.1):

что является выражением теоремы о кинетической энергии системы в дифференциальной форме.

Проинтегрировав (19.2.2) получаем:

- теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее конечном перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.

Подчеркнем, что внутренние силы не исключаются. Для неизменяемой системы сумма работ всех внутренних сил равна нулю и

Если связи, наложенные на систему, не изменяются со временем, то силы, как внешние так и внутренние, можно разделить на активные и реакции связей, и уравнение (19.2.2) теперь можно записать:

В динамике вводится такое понятие как "идеальная" механическая система. Это такая система, наличие связей у которой не влияет на изменение кинетической энергии, то есть

Такие связи, не изменяющиеся со временем и сумма работ которых на элементарном перемещении равна нулю, называются идеальными, и уравнение (19.2.5) запишется:

//изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.//

Билет №14.

Сила F, действующая на материальную точку М называется потенциальной (консервативной), если работа этой силы зависит только от начального и конечного положений точки М.

(Пример: гравитационные силы и силы упругости)

Диссипативными (неконсервативными) называются силы, зависящие от скоростей точек механической системы и совершающие отрицательную суммарную работу при любых перемещениях этой системы.

(Пример: силы трения скольжения, силы сопротивления движению).

Работа , совершаемая потенциальными силами при изменении конфигурации системы, то есть расположения ее частей (материальных точек) относительно системы отсчета, не зависит от того, как конкретно осуществляется процесс перехода из начальной конфигурации системы (1) в конечную (2). Работа полностью определяется начальной и конечной конфигурацией системы. Следовательно, ее можно представить в виде разности значений некоторой функции конфигурации системы , называемой потенциальной энергией системы:

= (1)- (2).

Соответственно элементарная работа потенциальных сил при малом изменении конфигурации системы

Если внешние потенциальные силы нестационарны, то потенциальная энергия системы зависит не только от конфигурации системы, но также и от времени . Между тем работу эти силы совершают только при перемещении системы. Поэтому данное соотношение справедливо лишь при условии стационарности внешних потенциальных сил. В общем случае:

Член показывает, как изменяется за малое время потенциальная энергия системы при условии, что конфигурация системы остается одной и той же. Измеряя работу потенциальных сил, приложенных к системе, можно найти только разность значений потенциальной энер­гии этой системы в двух ее состояниях: начальном и конечном. Иначе говоря, потенци­альную энергию системы можно найти только с точностью до произвольного постоян­ного слагаемого. В каждой конкретной задаче для получения однозначной зависимости потенциальной энергии рассматриваемой системы от ее конфигурации выбирают нуле­вую конфигурацию, в которой потенциальную энергию системы полагают равной нулю. Таким образом, потенциальной энергией механической системы называется вели­чина, равная работе, которую совершают все действующие на систему потенциальные силы при переводе системы из рассматриваемого состояния в состояние, соответст­вующее ее нулевой конфигурации.

Рассмотрим простейшую механическую системы, состоящую из одной материальной точки, на которую действует потенциальная сила F.

Так как координаты точки х, у, z — независимые переменные, то в последнем уравне­нии должны быть попарно равны слева и справа коэффициенты при dx, dy и dz. Таким образом, связь между потенциальной энергией материальной точки и соответствующей ей потенциальной силой F имеет

вид:

= , = , = ,

или

Вектор, стоящий в квадратных скобках и построенный с помощью скалярной функции , называется градиентом функции и обозначается grad .

.

Вид формулы потенциальной энергии зависит от характера взаимодействия тел.

Например, сила тяжести: , сила упругости .

Изменить могут гравитационные силы и силы упругости (в электростатике еще и кулоновские силы). Работа этих сил по замкнутой траектории всегда равна нулю. Такие силы называют консервативными.

Потенциальная энергия тела в положении равновесия.

( ).

( ).

( ).

( ).

Билет №15.

- в поле силы тяжести.

0

( ) = = = .

- в поле центральной силы.

Поле называется центральным, если сила, действующая на материальную точку, помещенную в это поле, направлена вдоль прямой, соединяющей ее с ее центром.

=0, так как ,

=

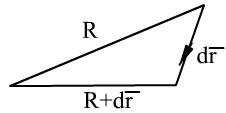
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т.е. найдем упругую энергию растянутой пружины.

Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила, с которой действует пружина, не остается постоянной при изменении растяжения. Мы видели (§ 37), что сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.

Значит, среднее значение силы равно F_ср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы:

A=1/2 kl•l=1/2kl².

Таким образом, потенциальная энергия упругости Е_п равна

E_п = 1/2 kl².          (98.1)

Здесь потенциальная энергия выражена через коэффициент упругости пружины и через наибольшее растяжение ее. Полученное выражение для потенциальной энергии можно записать и иначе, через величину силы упругости при наибольшем растяжении и коэффициент упругости:

          (98.2)

Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т. е. чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы, т. е. работа.

Это имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, погашая вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы будут меньше и конструкция самолета будет лучше предохранена от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке.

// Потенциальной энергией упругой деформации в сопротивлении материалов называется энергия, накопленная в теле вследствие упругих деформаций, вызванных действием внешних сил.

  Потенциальная энергия  u при статическом осевом растяжении или

сжатии стержня численно равна работе внешних сил.

 Интегрирование производится в пределах каждого участка, а суммирование - по всем участкам.

Если по длине l стержня величины N, А и Е постоянны, то: 

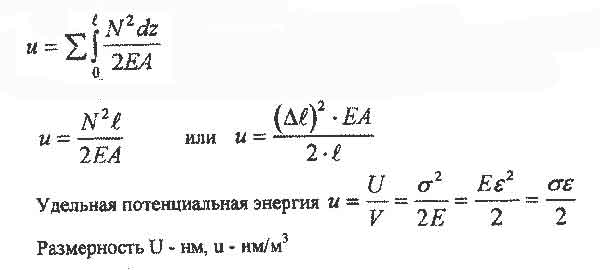
Билет № 16.

∆W_k=A_{всех сил} ∆W_п=-А_конс

∆W= A_{всех сил}- А_конс=A_неконс

ЗСМЭ

∆W=0 W=const A_неконс=0

Рассмотрим произвольную механическую систему, состоящую из n материальных точек. Ее кинетическая энергия , а изменение кинетической энергии равно сумме работ, совершаемых при этом всеми внешними и внутренними силами:

,

причем сумму элементарных работ всех сил, приложенных к материальной точке системы удобно разбить на две части:

.

Тогда

Из определения потенциальной энергии системы следует, что согласно

Величина W, равная сумме кинетической и потенциальной энергий системы, назы­вается механической энергией (полной механической энергией) системы. Уравнение выражает закон изменения механической энергии:

изменение механической энергии системы равно алгебраичес­кой сумме работ всех непотенциальных сил, действующих на систему, и изменения потенциальной энергии системы за рас­сматриваемый промежуток времени, обусловленного нестаци­онарностью внешних потенциальных сил.

Если система замкнута, то изменение ее механической энергии обусловлено только действием в ней непотенциальных сил:

Механическая система называется консервативной, если все действующие на нее

внешние и внутренние непотенциальные силы не совершают работы ( А^нпс = 0), а все внешние потенциальные силы стационарны. Потенциальная энергия консервативной системы может изменяться только при изменении конфигурации системы. Следовате­льно, частная производная по времени от потенциальной энергии консервативной системы, характеризующая быстроту изменения этой энергии с течением времени при условии постоянства конфигурации системы, тождественно равна нулю: .

Поэтому видно, что механическая энергия консервативной системы не изменяет­ся с течением времени.

Этот закон называется законом сохранения механической энергии. В частности, он справедлив для замкнутых консервативных систем: механическая энергия замкнутой системы не изменяется, если все внутренние силы потенциальны либо не совершают работы. Например, силы трения покоя и гироскопические силы работы не совершают. Поэтому действие таких сил на систему не вызывает изменения ее механической энергии.

Билет № 17.

ЗИИ

ЗСИ

Закон сохранения импульса (ЗСИ)- в инерциальной системе отсчета импульс замкнутой системы сохраняется. Или -сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

и

ЗИМИ

Закон изменения момента импульса.

 

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета.  L = ΣL_i.                                                           Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.   dL/dt = M.                                                      

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.

Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением

                                      .                                           

Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее.

В неинерциальной системе к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.

ЗСМИ

Закон сохранения момента импульса. Момент импульса сохраняется в замкнутой системе. Момент импульса относительно оси проходящей через начало координат-проекция вектора L на ось.

и

Билет №18.

Абсолютно неупругий удар – это столкновение двух тел, в результате которого тела объединяются и двигаются дальше, как единое целое. При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии ц ентров.

1.С-ма замкнута⇾ЗСИ

2 .ЗСМЭ

Частные случаи:

Абсолютно упругим ударом называется такой удар, при котором механическая энергия соударяющихся тел не преобразуется в другие виды энергии.

Пусть два абсолютно упругих шара массами

и движутся до удара поступательно со скоростями и , направленными вдоль оси ОХ, проходящей через центры шаров. Нужно найти скорости и шаров после соударения.

В процессе удара систему соударяющихся упругих тел можно считать замкнутой и консервативной. Следовательно, для решения этой задачи можно воспользоваться законами сохранения механической энергии и импульса. Перед ударом и после его завершения соударяющиеся тела не деформированы, так что потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Тогда из закона сохранения механической энергии имеем

По закону сохранения импульса:

Так как все скорости направлены по оси ОХ, то

(проекции векторов скоростей на ось ОХ)

Совместное решение уравнений дает

Окончательно получаем:

Билет №19.

Принцып относительности Галилея-все ИСО с механической точки зрения эквивалентны друг другу. Находясь внутри ИСО никакими способами нельзя определить покоится она или движется. Все законы механики во всех ИСО выполняются одинаково.

Рассмотрим две двумерные системы отсчёта. Одна система (плот) перемещается, вместе с перемещающимся по ней человеком, относительно другой. Δr(абсолютного перемещения, со значком вектора)= Δr(относительно системы координат с человеком, с значком вектора)+Δr(системы координат с человеком относительно главной системы координат, с значком вектора) так же это ур-ние справедливо если Δr заменить на скорость, ускорение//надо смотреть рисунок

Преобразования Галилея- в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной ИСО к другой. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета и выполнение принципа относительности.

Δy=Δy’

Δx=Δx’+υΔt

t=t’

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростяхдвижения, меньших скорости света в вакууме, в том числе близких кскорости света. В рамках специальной теории относительностиклассическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями.

Постулаты Эйнштейна: