Геометрическое толкование
а)
,
то есть
равен углу наклона касательной к y
= f
(x)
в точке
.
Обычный метод итераций, когда уравнений
приводит к виду
.
Рис.1.12
б) метод Ньютона – Рафсона.
Рис.1.13
Уравнение касательной
Пусть
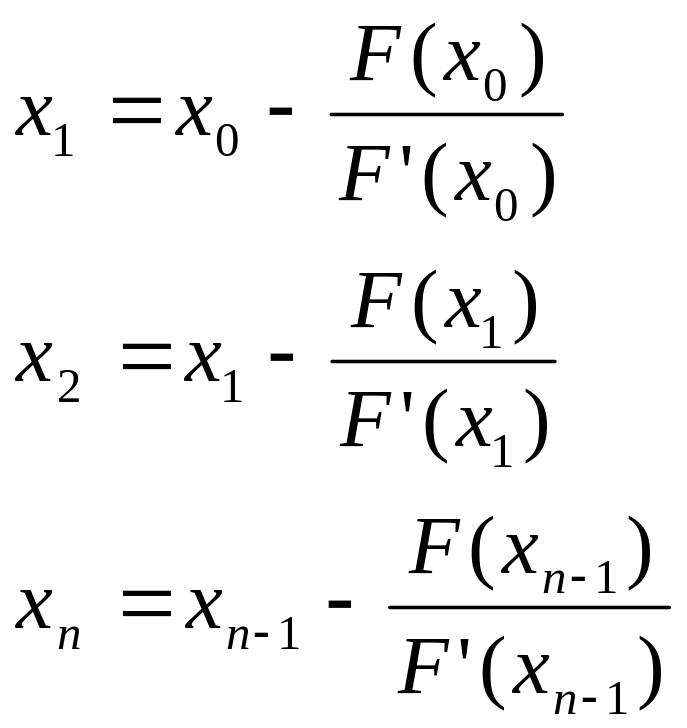
выбирать
так, чтобы
Пример:
F
(x)
= sin
x
– x
+ 0.15 = 0 на
отрезке [0.5; 1] с погрешностью
То
необходимо найти
чтобы
Рис.1.14
Это верно при = 1
на [0.5; 1]
Примечание:
если
,
то можно
1)
2)
3)
Вычисляем
4)
Проверяем
и так далее.
1.4. Случай почти равных корней
Рис.1.15
Производная
близка к 1 при
и на основании теоремы о среднем
,
при этом
.
Итерационный
процесс осциллирует
между
до бесконечности, не сходясь ни к одному
значению корня. Другими словами – не
удаётся отделить
эти два
корня, так как они расположены слишком
близко один к другому. Трудности
возникают, так как
.
Мейкон(1963) предложил метод, согласно
которому сначала находят значение x,
где
,
то есть решается уравнение:
.
Пусть
-
решение. Эта точка
.
Положим для начального приближения
.
Пусть
.
Разложим f(x)
в ряд Тейлора в окрестности точки
Так
как
Пусть
Но по условию
,
Если
,
так как надо решить уравнение
Рис.1.16
Сначала решаем:
.
Потом ищется:
.
Затем начальные приближения для
:
.
Если
,
то это означает что
имеет
более чем один корень вблизи
,
тогда сначала решается уравнение
,
то это означает, что
имеет более чем один корень
.
1.5. Метод хорд
Каждое значение xn+1 находится как точка пересечения оси абсцисс с хордой, проведенной через точки F(a) и F(b) , причем одна из этих точек фиксируется — та, для которой F(x)·F''(x)>0.
Если неподвижен конец хорды x = a, то
xn+1
= xn
-
Если неподвижен конец хорды x = b, то
xn+1
= xn
-
Если |xn+1 - xn|> ,то в первом случае считаем b = xn+1, во втором a = xn+1 и повторяем вычисление.
При использовании метода хорд полагается, что корень находится на отрезке [a,b].
1.6. Метод секущих
Реализуется алгоритмом, описанным выше, если абсцисса a и b взяты с одной стороны от корня.
Необходимость вычисления F'(x) и выбора одной из двух формул затрудняют практическое применение методов хорд и секущих в отдельности.
Рис.1.17
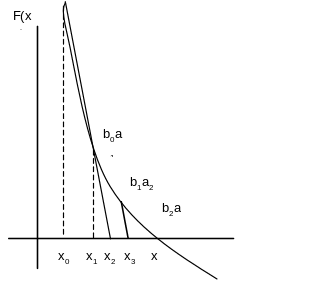
Рис.1.18
Варианты заданий
Необходимо вычислить приближенное значение корней уравнения с заданной точностью методом итераций и методом Ньютона-Рафсона. Необходимо построить график уравнений, отделить корни на соответствующих отрезках.
N варианта |
Уравнение |
Заданная точность ε |
1 |
|
10-3 |
2 |
|
10-2 |
3 |
|
10-3 |
4 |
|
10-2 |
5 |
|
10-3 |
6 |
|
10-2 |
7 |
|
10-3 |
8 |
|
10-2 |
9 |
|
10-3 |
10 |
|
10-2 |
11 |
|
10-2 |
12 |
|
10-3 |
13 |
|
10-2 |
14 |
|
10-3 |
15 |
|
10-2 |
16 |
|
10-3 |
17 |
|
10-2 |
18 |
|
10-3 |
