3.5. Форматирование Диаграммы

Щелкнем правой кнопкой мыши по названию оси Y, появится диалоговое окно, щелкнем по Формат названия оси, выберем закладку Выравнивание: по горизонтали – по центру, по вертикали – по центру. Перетащим название оси Y в левый верхний угол диаграммы около последнего значения координаты y. Перенесем название оси X в нижний правый угол диаграммы около последнего значения координаты х.

Щелкнем правой кнопкой мыши по центральному серому полю диаграммы – Область построения диаграмм. Появится диалоговое окно. Выберите Формат области построения. В закладке Вид выберем: Рамка невидимая, Заливка – прозрачная. Нажмите ОК.

Щелкнем правой кнопкой мыши по любой экспериментальной точке на диаграмме. Появится диалоговое окно. Выберите Формат рядов данных. В закладке Вид выберите: Линия – отсутствует, Маркер – обычный, тип маркера – треугольник, цвет – черный, фон – белый, размер 7 пт. Нажмите кнопку ОК.

Щелкнем правой кнопкой мыши по линии оси X. Появится диалоговое окно. Выберите Формат оси. Выберите закладку Вид: Ось – другая, Толщина – вторая снизу в раскрывающемся списке. Выберите закладку Шкала, установите минимальное значение, равное 0, максимальное – 2, цена основных делений – 0.5. Нажмите кнопку ОК.

Щелкнем правой кнопкой мыши по линии оси Y. Появится диалоговое окно. Выберите Формат оси. Выберите закладку Вид: Ось – другая, Толщина – вторая снизу в раскрывающемся списке. Выберите закладку Шкала, установите минимальное значение, равное 0, максимальное – 3, цена основных делений – 1. Нажмите кнопку ОК.

Щелкнем правой кнопкой мыши по линии ограничивающую область диаграммы. На линии появятся черные квадратные маркеры, потянув за которые можно изменить размер диаграммы. Также появится диалоговое окно в котором выберите Формат области диаграммы. В закладке Вид установите: Рамка – невидимая, Заливка – прозрачная. В закладке Шрифт уберите галку Автомасштабирование. Нажмите ОК.

6. На основании полученной таблицы экспериментальных данных найдем прямую по формуле , имеющую наименьшее среднее квадратичное отклонение от табличных значений, для этого составим систему (3.8). В случае линейной аппроксимации это система двух уравнений с двумя неизвестными – (3.13). Решение системы (3.13) сводится к расчету коэффициентов и свободных членов .

7. Рассчитаем коэффициенты и свободные члены :

После расчета коэффициентов воспользовавшись формулами (3.9) или табл. 3.2, найдем коэффициенты искомой прямой:

;

.

На основании полученных коэффициентов прямой рассчитаем теоретические значения , причем значения х возьмем прежние. Сформируем таблицу теоретических данных. Отобразим их на диаграмме.

Рассчитаем линейное суммарное среднеквадратичное отклонение по формуле (3.4).

Рассчитаем коэффициент корреляции (3.19).

'____________________линия

For i = 1 To h + 1

' Считывание таблицы экспериментальных данных

x(i) = Worksheets(1).Cells(i, 1).Value

y(i) = Worksheets(1).Cells(i, 2).Value

'Расчет коэффициентов S и свободных членов Т

S0 = S0 + 1

S1 = S1 + x(i)

S2 = S2 + x(i) * x(i)

T0 = T0 + y(i)

T0_11 = T0_11 + y(i) * y(i)

T1 = T1 + x(i) * y(i)

Next i

' Расчет коэффициентов прямой аппроксимации

a0 = -1 / (-S1 ^ 2 + S2 * S0) * (-S2 * T0 + S1 * T1)

a1 = (-S1 * T0 + T1 * S0) / (-S1 ^ 2 + S2 * S0)

'Расчет коэффициента корреляции

R1 = (S0 * T1 - S1 * T0)

R2 = Sqr((S0 * S2 - S1 * S1) * (S0 * T0_11 - T0 * T0))

R = R1 / R2

For i = 1 To h + 1

' Расчет таблицы теоретических данных

y1(i) = a0 + a1 * x(i)

' Расчет среднеквадратичной ошибки линейной аппроксимации

S_line = S_line + (y(i) - y1(i)) ^ 2

Next i

Вывод всех полученных данных осуществляем на рабочий лист 3.2 (табл 3.4).

На основе полученных данных получаем коэффициенты линейной аппроксимации: , .

Таким образом, уравнение искомой прямой (линейная аппроксимация табличной функции) есть . На основе этого уравнения получаем таблицу теоретических данных линейной аппроксимации. Для прямой коэффициент корреляции .

Таблица 3.4

i	S0	S1	S2	T0	T1	Sпрям
1	1	0	0	0.607833	0	0.0677
2	1	0.25	0.0625	0.638997	0.159749	0.000641
3	1	0.5	0.25	0.754814	0.377407	0.015597
4	1	0.75	0.5625	1.124718	0.843539	0.000442
5	1	1	1	1.143086	1.143086	0.072187
6	1	1.25	1.5625	1.634384	2.04298	0.001884
7	1	1.5	2.25	1.851189	2.776783	0.008581
8	1	1.75	3.0625	2.195643	3.842376	0.000202
9	1	2	4	2.755207	5.510413	0.07802
∑	9	9	12.75	12.70587	16.69633	0.245255

8. Найдем теперь аппроксимирующую кривую более высокого порядка – параболу .

В случае параболической аппроксимации это система трех уравнений с тремя неизвестными – (3.18). Решение системы (3.18) сводится к расчету коэффициентов и свободных членов .

9. Рассчитаем коэффициенты и свободные члены :

.

После расчета коэффициентов, воспользовавшись формулами (3.9) или таблицей 3.2, найдем коэффициенты искомой параболы:

;

;

.

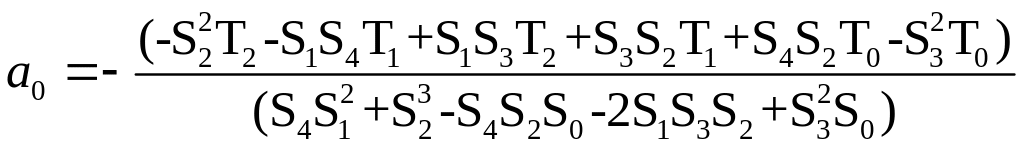На основании полученных коэффициентов параболы рассчитаем теоретические значения причем, значения х возьмем прежние. Сформируем таблицу теоретических данных (табл. 3.5). Отобразим их на диаграмме (рис. 3.3).

Таблица 3.5

x	yтеория
0	0.34764
0.25	0.613671
0.5	0.879702
0.75	1.145732
1	1.411763
1.25	1.677794
1.5	1.943825
1.75	2.209856
2	2.475887

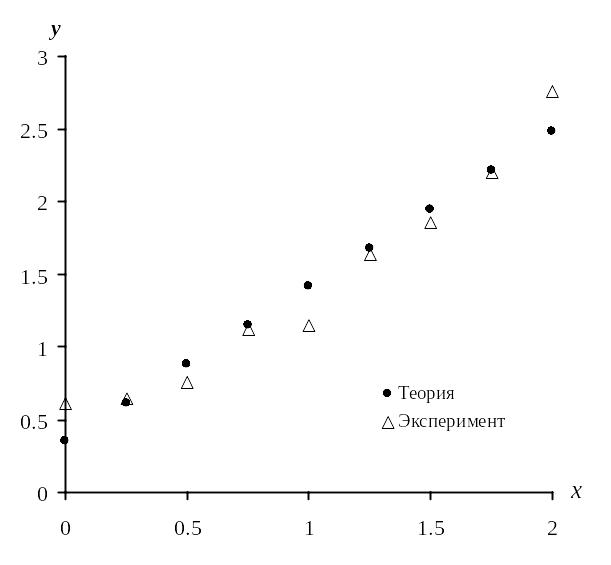
Рис. 3.3

Рассчитаем параболическое суммарное квадратичное отклонение по формуле (3.4).

'_____________________ парабола

For i = 1 To h + 1

' Считывание таблицы экспериментальных данных

x(i) = Worksheets(1).Cells(i, 1).Value

y(i) = Worksheets(1).Cells(i, 2).Value

' Расчет коэффициентов S и свободных членов T

S0 = S0 + 1

S1 = S1 + x(i)

S2 = S2 + x(i) * x(i)

S3 = S3 + x(i) * x(i) * x(i)

S4 = S4 + x(i) * x(i) * x(i) * x(i)

T0 = T0 + y(i)

T0_11 = T0_11 + y(i) * y(i)

T1 = T1 + x(i) * y(i)

T2 = T2 + y(i) * x(i) * x(i)

Next i

' Расчет коэффициентов параболической аппроксимации

а0 = -(-S2 ^ 2 * T2 - S1 * S4 * T1 + S1 * S3 * T2 + S3 * S2 * T1 + S4 * S2 * T0 - S3 ^ 2 * T0) / (S4 * S1 ^ 2 + S2 ^ 3 - S4 * S2 * S0 - 2 * S1 * S3 * S2 + S3 ^ 2 * S0)

а1 = (-S0 * S4 * T1 + S0 * S3 * T2 - S2 * S3 * T0 - S2 * T2 * S1 + S2 ^ 2 * T1 + T0 * S4 * S1) / (S4 * S1 ^ 2 + S2 ^ 3 - S4 * S2 * S0 - 2 * S1 * S3 * S2 + S3 ^ 2 * S0)

а2 = -(S3 * T0 * S1 - S3 * T1 * S0 - T2 * S1 ^ 2 + S2 * T1 * S1 - S2 ^ 2 * T0 + S2 * S0 * T2) / (S4 * S1 ^ 2 + S2 ^ 3 - S4 * S2 * S0 - 2 * S1 * S3 * S2 + S3 ^ 2 * S0)

For i = 1 To h + 1

'Расчет таблицы теоретических данных

y2(i) = b0 + b1 * x(i) + b2 * x(i) * x(i)

'Расчет параболического суммарного квадратичного отклонения

S_parab = S_parab + (y(i) - y2(i)) ^ 2

Next i

Вывод всех полученных данных осуществляем на рабочий лист 3.

На основе полученных данных получаем коэффициенты параболической аппроксимации: , , .

Таким образом, уравнение искомой параболы (параболической аппроксимация табличной функции) есть

.

На основе этого уравнения получаем таблицу теоретических данных параболической аппроксимации.

Для параболы .

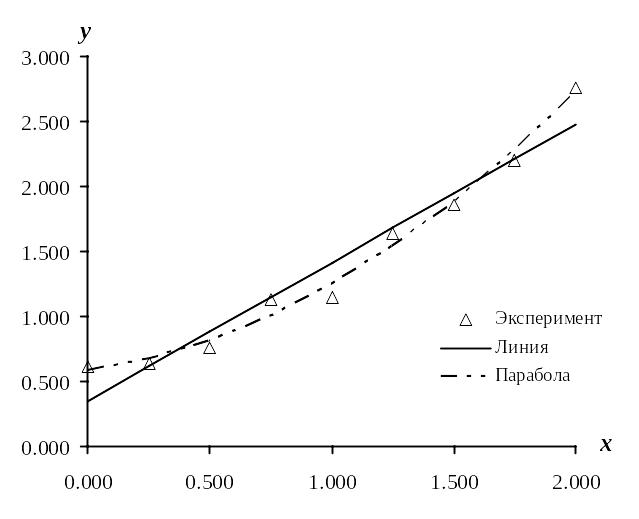
Рис. 3.4

10. Вывод итоговых данных осуществляем на рабочий лист 4 – таблицы: экспериментальных данных, линейной и параболической аппроксимаций, линейное и параболическое суммарное квадратичное отклонения, общую диаграмму (Рис. 3.4) .

Таблица 3.6

i	S0	S1	S2	S3	S4	T0	T1	T2	Sпарабола
1	1	0	0	0	0	0.607833	0	0	0.0005711
2	1	0.25	0.0625	0.015625	0.003906	0.638997	0.159749	0.039937	0.0011389
3	1	0.5	0.25	0.125	0.0625	0.754814	0.377407	0.188703	0.0032919
4	1	0.75	0.5625	0.421875	0.316406	1.124718	0.843539	0.632654	0.014994
5	1	1	1	1	1	1.143086	1.143086	1.143086	0.0099792
6	1	1.25	1.5625	1.953125	2.441406	1.634384	2.04298	2.553725	0.0100108
7	1	1.5	2.25	3.375	5.0625	1.851189	2.776783	4.165174	0.0006312
8	1	1.75	3.0625	5.359375	9.378906	2.195643	3.842376	6.724158	0.0053708
9	1	2	4	8	16	2.755207	5.510413	11.02083	0.0018512
∑	9	9	12.75	20.25	34.26563	12.70587	16.69633	26.46826	0.0478391

Таким образом,

,

в тоже время для прямой

.

То есть

.

Сравнение прямой, параболы и экспериментальных точек подтверждает вывод, что в данном случае парабола заметно лучше аппроксимирует функциональную зависимость, полученную в эксперименте, чем прямая.