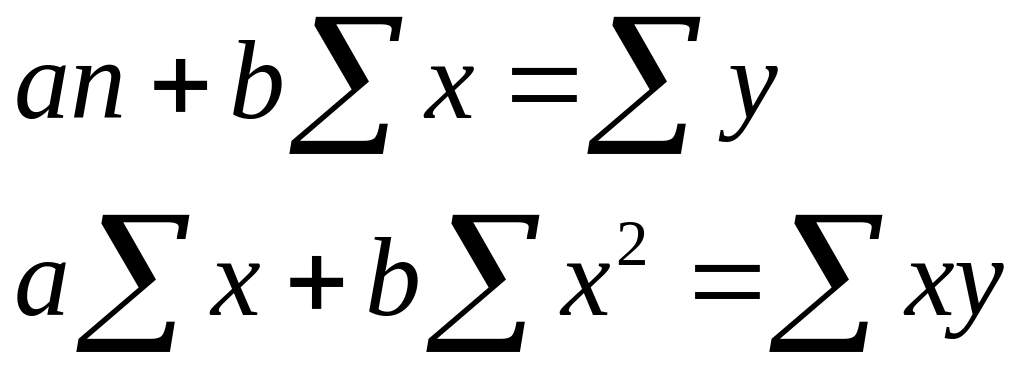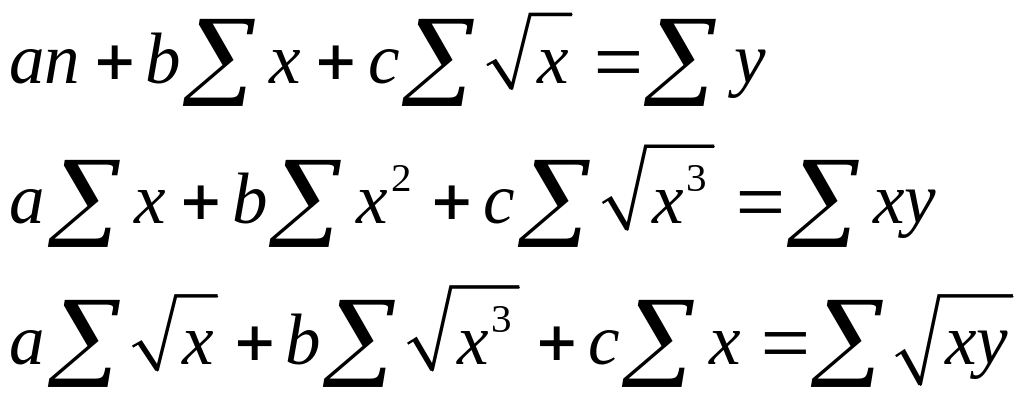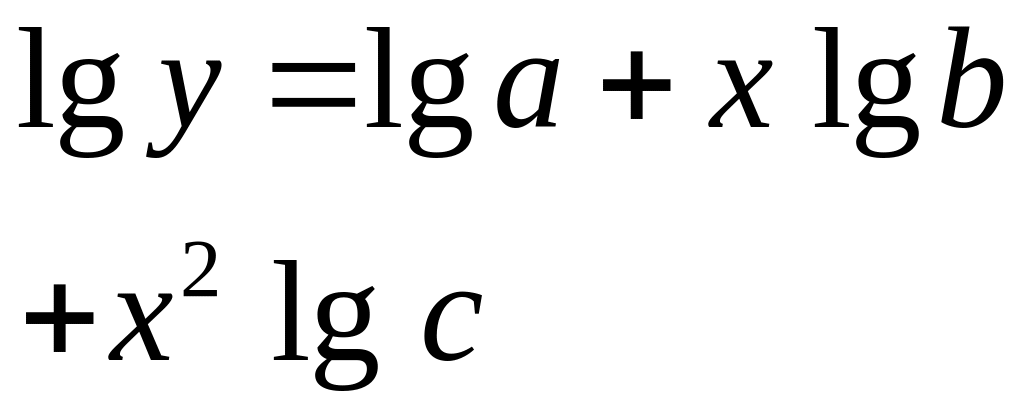3.2.Вычислительная схема метода наименьших квадратов

Метод наименьших квадратов, с помощью которого могут быть успешно решены задачи рассмотренных типов, заключается в следующем.

Рассмотрим сумму квадратов разностей значений , даваемых экспериментом, а значений аппроксимации при соответствующих аргументах :

.

(3.4)

Наша цель – подобрать параметры , и так, чтобы эта сумма имела наименьшее значение (иначе: сумма квадратов отклонений вдоль оси OY должна быть минимальной (принцип Лежандра):

.

(3.5)

Таким образом задача свелась к нахождению минимума функции , который определяется вполне конкретным набором фиксированных аргументов , , … .

Известные методы минимизации функционала (3.4) приводят к следующей системе нормальных уравнений:

.

(3.6)

Выберем в качестве приближающей функции многочлен , то есть совокупности табличных значений поставим в соответствие следующий полином степени :

.

(3.7)

При такой аппроксимации минимизирующие условия (3.6) выполняются, если коэффициенты удовлетворяют системе линейных уравнений с неизвестными.

.

(3.8)

Числовые коэффициенты и свободные члены системы (8) определяются при помощи формул:

,

(3.8/)

где значения и берутся из табл. 3.1 экспериментальных результатов.

Для нахождения коэффициентов воспользуемся формулами Крамера, тогда

,

(3.9)

здесь 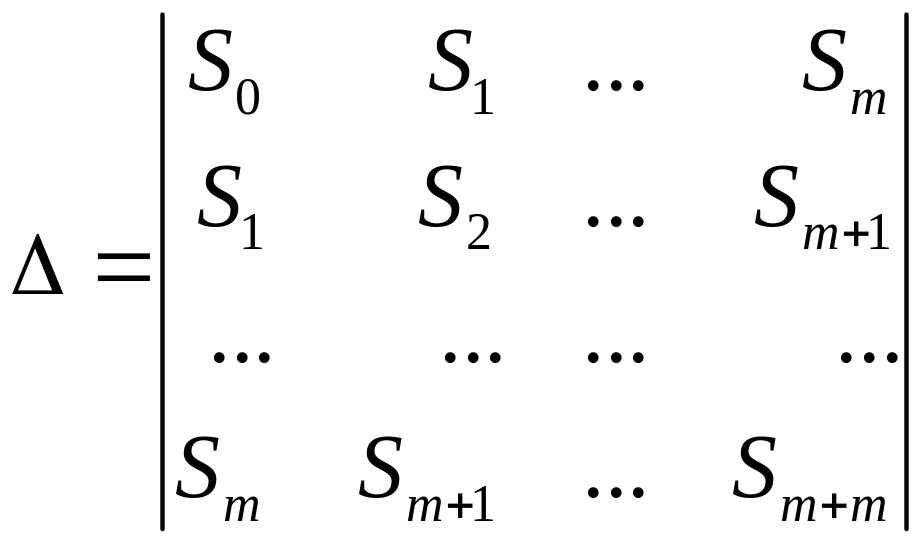– определитель системы ; – определитель, полученный из определителя системы заменой i-го столбца столбцом из свободных членов ( ).

Рассмотрим несколько случаев определения функции .

Пусть . Функции в этом случае имеет вид:

.

(3.10)

Это функция с двумя переменными и ( и – заданные числа (табл. 3.1).

,

(3.11)

то есть система уравнений в этом случае принимает вид:

.

(3.12)

Получили систему двух линейных уравнений с двумя неизвестными и . Очевидно, что система имеет определенное решение и что при найденных значениях и функция имеет минимум.

Перепишем систему (3.12) в виде (3.8):

,

(3.13)

где в соответствии с формулами (3.8^/):

Пусть за аппроксимирующую функцию взят многочлен второй степени:

.

(3.14)

В этом случае выражение (3.4) имеет вид:

.

(3.15)

Это функция трех переменных , , . Система уравнений (3.6) принимает вид:

(3.16)

или в развернутом виде:

.

(3.17)

Получаем систему линейных уравнений для определения неизвестных , , . Из характера задачи следует, что система имеет определенное решение и что при полученных значениях функция имеет минимум.

Перепишем систему (3.17) в виде (3.8)

,

(3.18)

где в соответствии с формулами (3.8^/):

.

Обратим внимание, что параметры

переходят в систему (3.18) из аппроксимации более низкого порядка (3.13). В этом существенное вычислительное преимущество метода наименьших квадратов – при построении аппроксимаций более высокого порядка используются результаты предыдущих аппроксимаций.

Оценка степени связи при аппроксимации данных линейной зависимостью производится на основе подсчета коэффициента корреляции . В случае, если связь между и может быть представлена прямой линией, коэффициент корреляции , если связи между переменными вообще не существует, то .

Коэффициент парной корреляции подсчитывается по формуле:

(3.19)

Принято считать:

при – слабая связь,

при – средняя связь,

при – сильная связь,

при – весьма сильная связь.

Приведем таблицу наиболее употребимых функций и соответствующих им систем нормальных уравнений (табл. 3.2).

Таблица 3.2

№	Функция	Нормальные уравнения	Решения уравнений
1
2
3
4

Продолжение табл. 3.2

№	Функция	Нормальные уравнения	Решения уравнений
5	или
6
7
8	или

Примечание к табл. 3.2.

;

;

;

;

;

;

;

;

;

;

;

;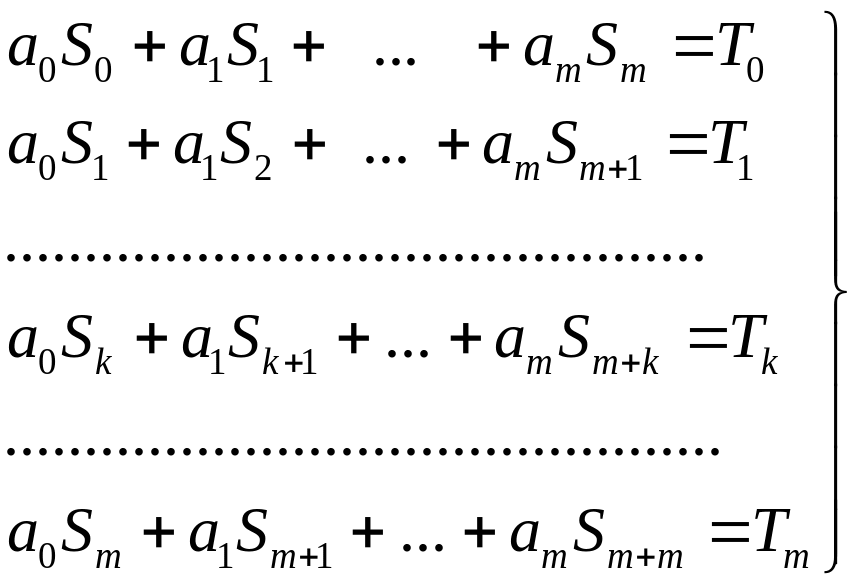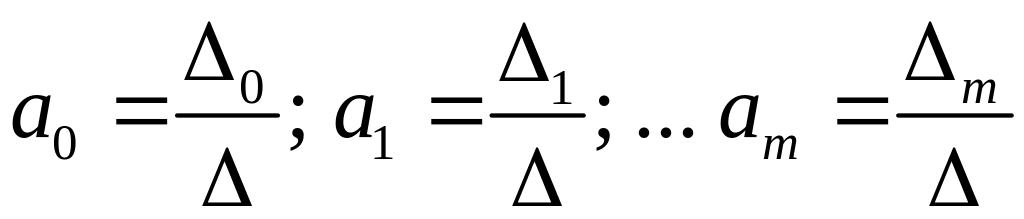