Электрическая ёмкость. Конденсаторы. Соединение конденсаторов. Энергия заряженного конденсатора. Объемная плотность энергии электрического поля.

Электроемкость определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.

Емкость проводника зависит от его размера и формы, но не зависит от материала, агрегатного состояния, формы и размеров полости полостей внутри проводника. Емкость не зависит от заряда проводника и его потенциала.

Единица электроемкости — фарад(Ф).

Конденсаторы — устройства обладающие небольшими размерами и потенциалами умеющие накапливать значительные по величине заряды, то есть обладающие большой емкостью.

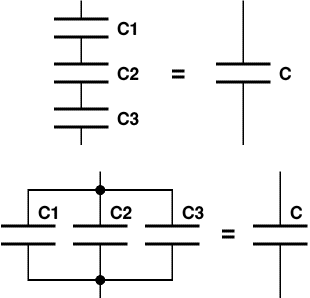
Соединения конденсаторов.

Параллельное соединения конденсаторов.

У параллельно соединенных конденсаторов разность на ободках одинакова и равна

Заряд отдельных конденсаторов равен

Полная емкость батареи при параллельном соединении равна сумме емкостей отдельных конденсаторов:

Последовательно соединение конденсаторов.

У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов

Полная емкость батареи в данном случае равна:

Энергия заряженного конденсатора.

где Q – заряд конденсатора, С — его емкость, - разность потенциала между обкладками конденсатора.

Объемная энергия электростатического поля - Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему.

Эта формула справедлива только для изотропного диэлектрика.

Закон сохранения момента импульса. Кинетическая энергия вращающегося тела.

1.Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r — радиус-вектор, проведенный из точки О в точку А;p=mv – импульс материальной точки;L – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p.

Модуль вектора момента импульса

где α – угол между векторами r и p, l – плечо вектора p относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момент импульса, определенного относительно произвольной точки О данной оси. Момент импульса не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью .Скорость и импульс перпендикулярны этому радиусу, т.е радиус является плечом вектора .Поэтому можем записать, что момент импульса отдельной частицы равен

Закон сохранения импульса — фундаментальный закон природы. Он связан со свойствами симметрии в пространстве — его изотропностью, т.е с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.

Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского.

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:

где Jz – момент инерции тела относительно оси z. Таким кинетическая энергия вращающегося тела

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

Где m - масса катящегося тела; vc – скорость центра масс тела;Jc – момент инерции тела относительно оси, проходящей через его центр масс;ω — угловая скорость тела.