Связь напряженности с потенциалом. Эквипотенциальные поверхности и их ортогональность силовым линиям.

Работа по перемещению единичного точечного заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и , равна . Та же работа равна .

Приравняв оба выражения получим

где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей y и z получим

где I,k,j единичные векторы.

т.е напряженность поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Для графического изображения распределения потенциала электростатического поля, как и в случае тяготения пользуются эквипотенциальными поверхностями.

Эквипотенциальные поверхности — это поверхности, во всех точках которых потенциал φ имеет одно и тоже значение.

Линии напряженности в случае точечного заряда — радиально прямые. Следовательно линии напряженности в случае точечного заряда перпендикулярны эквипотенциальной поверхности.

Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал , поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т.е электростатические силы, действующие на заряд, всегда направлены по нормали к эквипотенциальным поверхностям. Следовательно вектор Е всегда нормален к эквипотенциальным поверхностям, поэтому линии вектора Е ортогональны этим поверхностям.

Зная расположение линий напряженности электростатического поля, можно построить эквипотенциальную поверхность и , наоборот, по известному положению эквипотенциальных поверхностей можно определить в каждой точке модуль и направление напряженности поля.

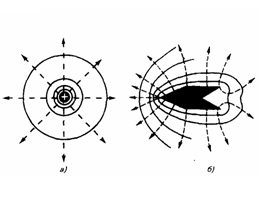
а)Вид линий напряженности(штрих. Линии) и эквипотенциальных поверхностей(сплошные линии) полей положительного точечного заряда.

б)Занаряженный металлический цилиндр, имеющий на одном конце выступ, а на другом впадину.

Основные понятия динамики вращательного движения( момент инерции, теорема Штейнера, момент импульса, момент силы). Основной закон динамики вращательного движения.

Моментом инерции системы относительно данной оси называет физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояния до рассматриваемой оси:

Теорема Штейнера — момент инерции J тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

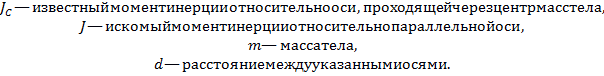
Иллюстрация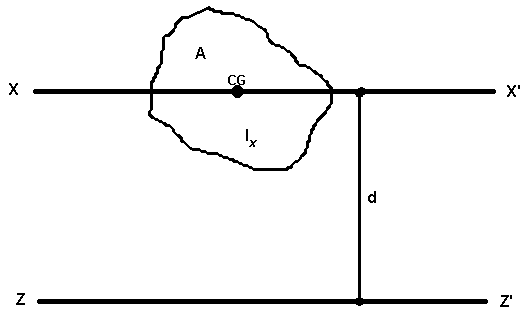

Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r — радиус-вектор, проведенный из точки О в точку А;p=mv – импульс материальной точки;L – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p.

Модуль вектора момента импульса

где α – угол между векторами r и p, l – плечо вектора p относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момент импульса, определенного относительно произвольной точки О данной оси. Момент импульса не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью .Скорость и импульс перпендикулярны этому радиусу, т.е радиус является плечом вектора .Поэтому можем записать, что момент импульса отдельной частицы равен

Момент импульса твердого тела относительно оси есть сумма моментов импульса его отдельных частиц.

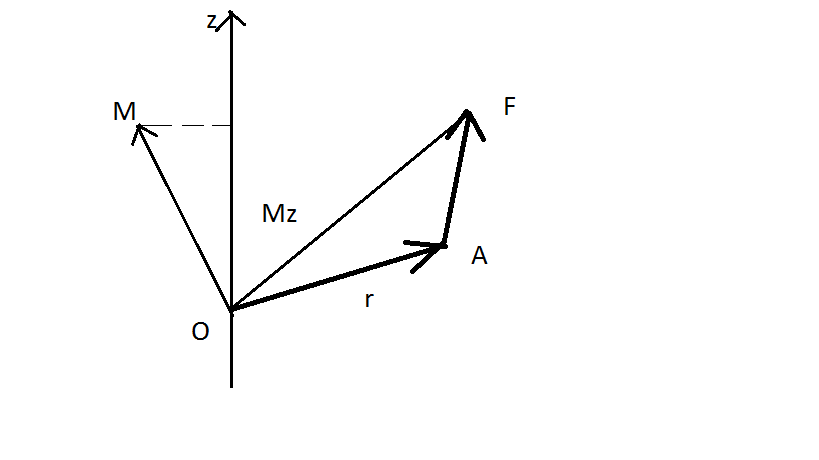
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектра r, проведенного из точки О в точку А приложения силы F:

Здесь M – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F.

Модуль момента силы

где α — угол между r и F;rsinα= l – кратчайшее расстояние между линией действия силы и точки О — плечо силы.

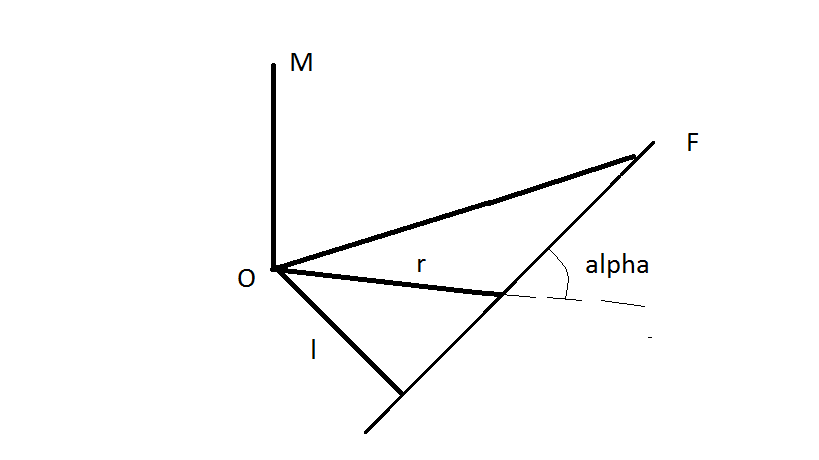
Момент силы относительно неподвижной оси z – скалярная величина Mz, равная проекции на эту ось вектора M момента силы, определенного относительно произвольной точки О данной оси. Значение момента Mz не зависит от выбора положения точки О на оси z.

Основной закон динамики вращательного движения - импульс момента силы, действующий на вращательное тело, равен изменению его момента импульса.