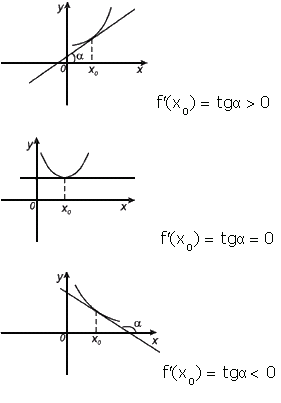1)Непрерывность функции в точке.

 

            Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.

 

Тот же факт можно записать иначе:

 

            Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.

 

Пример непрерывной функции:

 

 

 

                                                           y

 

                                               f(x0)+e

                                                  f(x0)

                                               f(x0)-e

 

0  x0-D   x0 x0+D                                  x

    

Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

верно неравенство                               .

 

            Определение.  Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.

 

f(x) = f(x0) + a(x)

где a(х) – бесконечно малая при х®х0.

 

 Свойства непрерывных функций.

 

1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.

 

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.

 

            3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x),  v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.

 

            Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.

2)Односторонние пределы

Пусть переменная  x  стремится к  a, оставаясь больше  a, и при этом   . Тогда число  A  называют правосторонним пределом (или пределом справа) функции     и обозначают любым из символических выражений Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае     при  x → a  со стороны меньших значений: Для существования обычного (двустороннего) предела функции     в точке  a  необходимо и достаточно равенство между собой односторонних пределов: Например, в точке  x = 3  односторонние пределы функции отличаются друг от друга: Поэтому в рассматриваемой точке предел функции     не существует. Классификация точек разрыва функции   Точка х0 называется точкой разрыва функции f (x), если f (x) в точке х0 не является непрерывной.   Это значит, что или не существует предела функции в данной точке, или этот предел не совпадает с тем значением, которое функция принимает в этой точке.   Точка х0 называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы   Точка х0 называется точкой разрыва второго рода функции f(x), если в этой точке функция f (x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.   Так для функции в точке х = 0 односторонние пределы равны , то х = 0 является точкой разрыва второго рода.

4)Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции  y=f(x) в этой точке Уравнение касательной к графику функции y=f(x) в точке x0 : Физический смысл производной. Если точка движется вдоль оси х и ее координата изменяется по закону  x(t), то мгновенная скорость точки:

Уравнение касательной и нормали к графику функции в точке

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:

y/(x)=limΔx→0ΔxΔy

Δy=f(x+Δx)−f(x). 

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

Уравнение нормали

Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).