Тема 1. Линейные автоматические системы

Лекция 2. Структурный анализ Линейных стационарных систем

2.1 Передаточная функция линейной стационарной системы

Любая система управления представляет собой совокупность нескольких устройств, в которых происходят явления различной физической природы. Одна и та же система может включать в себя, например, механические, электрические, пневматические и гидравлические элементы.

Эти черты системы взаимодействуют между собой по сложным законам механики, электротехники, гидравлики.

Будем рассматривать элементы, в которых процессы преобразования энергии строго ориентированы, то есть энергия и воздействия передаются только в определенном направлении, обладают детектирующим свойством. Это означает, что выходная величина элемента не влияет на свою входную.

Обычно свойством однонаправленности обладают те элементы системы, которые передают информационные воздействия. К таким элементам относятся измерители и преобразователи сигналов.

Первым этапом при исследовании или конструировании системы управления является составление математического описания ее элементов и системы в целом.

Составление математического описания конструктивного элемента системы управления состоит из следующих последовательно выполняемых процедур: принятие определенных допущений, выбор входных и выходных переменных, выбор системы отсчета для каждой переменной, применение физического принципа, отражающего в математической форме закономерности преобразования энергии или вещества.

Наиболее распространенной формой описания передаточных свойств систем управления и их элементов являются обыкновенные дифференциальные уравнения.

Для элемента, имеющего один входной X(t) и один выходной Y(t) сигнал, обыкновенное дифференциальное уравнение записывается в общем случае следующим образом:

Уравнение называют уравнением динамики или уравнением движения элемента. При этом понятие «движение» употребляется в самом обобщенном смысле.

Уравнение может быть линейным и нелинейным. В него, кроме основных переменных, входят постоянные величины, называемые параметрами.

Числовые значения параметров зависят от конструктивных данных описываемого элемента – масс, индуктивностей, емкостей и т.д.

Если переменная Y, характеризующая состояние элемента, кроме времени зависит еще от другой независимой переменной, которая является пространственной координатой, то элемент описывается дифференциальным уравнением с частными производными. Сам элемент в этом случае называют элементом с распределенными параметрами (распределенными в пространстве).

Большинство объектов управления представляют собой объекты с распределенными параметрами, но при практических расчетах с большей или меньшей степенью приближения их рассматривают как элементы с сосредоточенными параметрами.

Рассмотрим элемент системы управления с несколькими входными и выходными переменными. Такие элементы называют многомерными. Многомерными элементами являются прежде всего сами объекты управления. Например, электрический генератор переменного тока имеет две выходные переменные – напряжение и частоту и две входные переменные – напряжение возбуждения и частоту вращения генератора. Многомерными элементами могут быть сложные управляющие устройства в виде микроЭВМ, микроконтроллеров, выполняющих роль многоканальных регуляторов.

В приведенном примере выходные переменные генератора являются реальными физическими величинами, которые, как правило, поддаются измерению. Однако, как будет показано ниже, в качестве выходных переменных могут фигурировать некоторые абстрактные переменные, например производные от реальных выходных переменных, не имеющие конкретного физического смысла, и тогда даже элемент с одним входом и одним выходом, но описываемый дифференциальным уравнением выше первого порядка, может рассматриваться как многомерный.

Математическое описание передаточных свойств любых линейных многомерных элементов может быть осуществлено в двух различных видах:

• при помощи динамических характеристик (дифференциальных уравнений, временных, передаточных и частотных функций), записанных для реальных входных и выходных переменных;

• при помощи дифференциальных уравнений в форме Коши, записанных для абстрактных выходных переменных (переменных состояния).

Обозначим для краткости первый способ ВВ (вход – выход), а второй – ПС (переменные состояния).

Способ описания “вход – выход”

Пусть имеется многомерный элемент (рис.2.1) с m входными переменными

Рис. 2.1. Многомерный элемент с n измеряемыми (наблюдаемыми) выходными переменными

В общем случае каждая входная переменная связана с каждой выходной переменной.

Если взаимосвязи по всем каналам  линейны или линеаризованы, то в общем случае элемент можно описать следующей системой n неоднородных дифференциальных уравнений:

= 2.1

Заметим, что совпадение наивысшего порядка m производной с числом входных переменных является условным.

Систему автоматического управления можно представить в виде соединения звеньев. Для анализа работы САУ необходимо иметь зависимости, связывающие входные и выходные сигналы звеньев. Эти зависимости определяются с помощью дифференциальных уравнений.

Рассмотрим простейший случай линейного звена непрерывного действия, у которого все процессы описываются с помощью линейных дифференциальных уравнений. Связь между выходной (Y) и входной (X) величинами линейного звена или линейной системы выражается линейным дифференциальным уравнением с постоянными коэффициентами.

Для описания свойств звеньев более удобно пользоваться не непосредственно дифференциальными уравнениями, а следующими коэффициентами или функциями, вытекающими из уравнения (2.1) и также полно определяющими связь между входной и выходной величинами звеньев:

• передаточной функцией;

• переходной характеристикой (функцией);

• комплексным коэффициентом передачи (ККП).

Удобной формой записи линейных дифференциальных уравнений является символическая или операторная.

Переход к этой форме осуществляется введением сокращенного условного обозначения операции дифференцирования.

Преобразование Лапласа основано на двух следующих формулах: - прямого преобразования Лапласа

(2.2)

- обратного преобразования Лапласа

.

(2.3)

Здесь - обозначения прямого и обратного преобразования Лапласа. Преобразованная по Лапласу величина называется изображением и обозначается через соответственно для входной и выходной величин. Под " " подразумевается комплексная частота . Если , преобразование Лапласа превращается в его частный случай - преобразование Фурье.

В справочниках по математике имеются таблицы преобразования Лапласа для различных функций, встречающихся в практических задачах.

Передаточной функцией линейного звена K(p) называется отношение изображения выходной величины Y(p) к изображению входной величины X(p) при нулевых начальных условиях, т.е. при отсутствии запаса энергии в звене :

2.4

Рассматривая линейное дифференциальное уравнение (2.1) и находя изображение для левой и правой частей уравнения, получаем

2.5

Отсюда

2.6

Определение 2.1. Отношение изображения по Лапласу выходного сигнала к входному сигналу, определенно при начальных нулевых условиях, называется передаточной функцией.

Передаточная функция так же, как и дифференциальное уравнение, полностью определяет динамические свойства автоматической системы. Зная передаточную функцию АС и изображение входного сигнала, легко найти изображение выходного сигнала:

2.7

Из выражения (2.7), используя обратное преобразование Лапласа, получим

2.8

Передаточная функция не зависит от вида входного сигнала и полностью определяется структурой и параметрами линейной системы.

Рассмотрим основные свойства передаточной функции. Из выражения (2.6) видно, что в общем случае передаточная функция представляет собой дробно-рациональную функцию комплексного переменного «р». Обозначим

Полином в числителе передаточной функции:

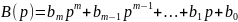2.9

Полином в знаменателе передаточной функции

2.10

Корни уравнения В(р)=0 называются нулями передаточной функции. Корни уравнения А(р)=0 называются полюсами передаточной функции.

Из теории обыкновенных дифференциальных уравнений с постоянными коэффициентами известно, что уравнение

2.11

Представляет собой характеристическое уравнение дифференциального уравнения (2.1).

Корни характеристического уравнения (2.11) позволяют определить общее решение однородного дифференциального уравнения

2.12

Это решение определяет поведение АС при отсутствии внешних воздействий, т.е. свободное движение системы. С характером свободного движения АС тесно связаны такие фундаментальные автоматики как устойчивость и качество процесса регулирования. Поэтому в теории автоматического управления большое значение придается исследованию полюсом передаточной функции, а полином (2.10) называют характеристическим полиномом автоматической системы.
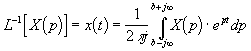