Int main()

{

int x,y,i;

struct tree *root;

struct tree *node_2, *node_3, *node_5;

struct tree *node_8, *node_9, *node_6,*node_10,*node_4, *node_7 ;

//создание дерева

root = NULL;

root = my_insert(root,1,0);

node_2 = my_insert(root,2,0);

node_3 = my_insert(root,3,1);

node_4 = my_insert(root,4,2);

node_5 = my_insert(node_3,5,0);

node_8 = my_insert(node_5,8,0);

node_9 = my_insert(node_5,9,2);

node_6 = my_insert(node_3,6,2);

node_10 = my_insert(node_6,10,1);

node_7 = my_insert(node_4,7,1);

//выполнение обхода дерева различными способами

preorder(root);

printf("\n");

inorder(root);

printf("\n");

postorder(root);

return 0;

}

16) Обход в ширину- это обход вершин дерева по уровням, начиная от корня, слева направо (или справа налево).

Алгоритм обхода дерева в ширину

Шаг 0:

Поместить в очередь корень дерева.

Шаг 1:

Взять из очереди очередную вершину. Поместить в очередь всех ее сыновей по порядку слева направо (справа налево).

Шаг 2:

Если очередь пуста, то конец обхода, иначе перейти на Шаг 1.

Поиск в ширину реализуется с помощью структуры очередь. Для этого занесем в очередь исходную вершину. Затем будем работать, пока очередь не опустеет, таким образом: выберем элемент из очереди и добавим все смежные ему элементы, которые еще не использованы.

18)

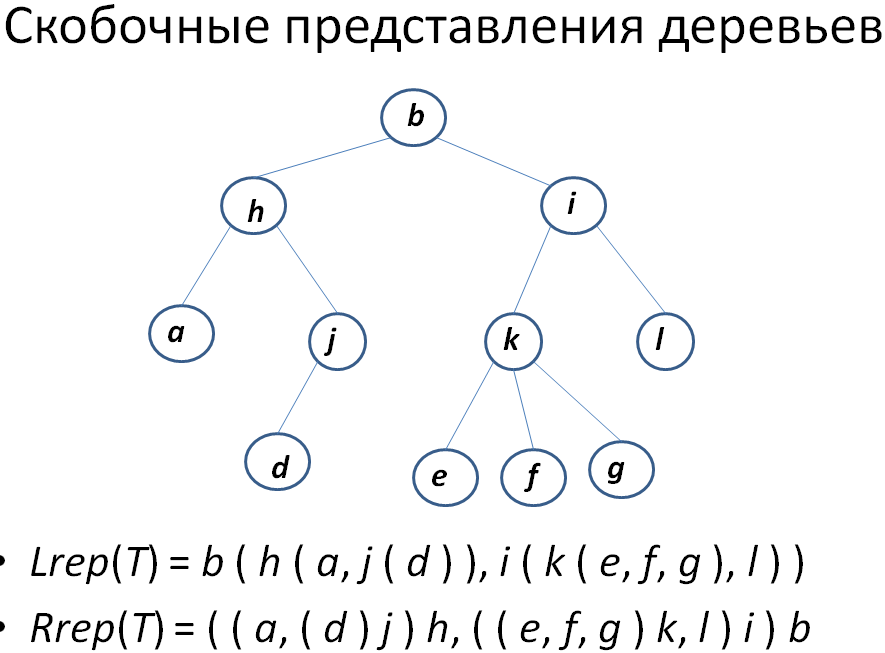
19)Деревья двоичного поиска .Определение. Деревом двоичного поиска для множества S называется помеченное двоичное дерево, каждый узел v которого помечен элементом l(v)ÎS так, что

1. l(u) < l(v) для каждого узла u из левого поддерева узла v,

2. l(w) > l(v) для каждого узла w из правого поддерева узла v,

3. для любого элемента a ÎS существует единственный узел v , такой что l(v) = a.

Алгоритм просмотра дерева двоичного поиска

Вход: Дерево T двоичного поиска для множества S, элемент a.

Выход: true если aÎS, false - в противном случае.

Метод: Если T = Æ, то выдать false, иначе выдать ПОИСК (a, r), где r – корень дерева T.

функция ПОИСК (a, v) : boolean

{

если a = l(v) то выдать true

иначе

если a < l(v) то

если v имеет левого сына w

то выдать ПОИСК (a, w)

иначе выдать false;

иначе

если v имеет правого сына w

то выдать ПОИСК (a, w)

иначе выдать false;

19) Реализация бинарных деревьев на Си

typedef struct node {

char *word;

struct node *left;

struct node * right;

} tree;

void print_tree (tree *t)

{

if (!t) return;

print_tree(t->left);

printf (“%s\n”, t->word);

print_tree(t->right);

}

21)Сбалансированые деревья Теорема.

Среднее число сравнений, необходимых для вставки n случайных элементов в дерево двоичного поиска, пустое в начале, равно O(n log₂n) для n ≥ 1 .

(без доказательства).

Максимальное число сравнений O(n²) – для вырожденных деревьев.

Определение.

Дерево называется сбалансированным тогда и только тогда, когда высоты двух поддеревьев каждой из его вершин отличаются не более чем на единицу.

Вставка элемента в сбалансированное дерево

Пусть r – корень, L – левое поддерево, R – правое поддерево. Предположим, что включение в L приведет к увеличению высоты на 1.

Возможны три случая:

1. h_L = h_R

2. h_L < h_R

3. h_L > h_R →нарушен принцип сбалансированности, дерево нужно перестраивать

₂₂₎ Поиском в глубину называется способ обхода вершин графа, который, начавшись от какой-либо вершины, рекурсивно применяется ко всем вершинам, в которые можно попасть из текущей

При поиске в ширину вместо стека рекурсивных вызовов хранится очередь, в которую записываются вершины в порядке удаления от начальной.  В глубину

Пусть задан граф  , где   — множество вершин графа,   — множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены вбелый цвет. Выполним следующие действия:

1. Из множества всех белых вершин выберем любую вершину, обозначим её  .

2. Выполняем для неё процедуру DFS( ).

3. Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.

Процедура DFS (параметр — вершина  )

1. Перекрашиваем вершину 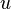  в черный цвет.

2. Для всякой вершины  , смежной с вершиной u и окрашенной в белый цвет

23) Каркасом, или остовным деревом для этого графа называется связный подграф этого графа, содержащий все вершины графа и не имеющий циклов. Количество ребер в каркасе связного графа всегда на единицу меньше количества вершин графа.

Ясно, что у графа может быть несколько каркасов. Например, различные каркасы можно построить, запуская поиск в глубину от разных вершин графа. Назовем стоимостью каркаса сумму весов ребер, входящих в него. На рисунке изображен граф и два его каркаса.

25) Шарниром в теории графов называется вершина графа, при удалении которой количество компонент связности возрастает. Для обозначения этого понятия также используются термины «разделяющая вершина» и «точка сочленения». С понятием шарнира также связано понятие двусвязности. Связный граф, не содержащий шарниров, называется двусвязным. Максимальный двусвязный подграф графа называется компонентой двусвязности. Компоненты двусвязности иногда называют блоками.

Сформулируем алгоритм поиска точек сочленения более строго. Реализуем рекурсивную функцию void go(int curr, int prev), где curr — текущая вершина, а prev — вершина, из которой мы попали в текущую. При первом вызове curr = r, prev = –1. В теле функции будут выполняться следующие шаги:

1. Запишем в number[curr] номер вершины curr в порядке обхода в глубину.

2. Запишем в L[curr] значение number[curr].

3. Переберем в цикле все вершины, в которые есть ребро из curr. Для каждой такой вершины i выполним следующие действия:

   1. Если вершина i еще не посещена, вызовем рекурсивно функцию go с параметрами i, curr. Если после этого значение L[i] стало меньше, чем L[curr], присвоим L[curr] = L[i].

   2. Если вершина i уже была посещена и ее номер number[i] < number[curr], и при этом i не равно prev (т.е. ребро (i, prev) обратное и возвращается в вершину с меньшим номером), то если L[curr] > number[i], присвоим L[curr] = number[i].

Данный алгоритм заполнит массивы L[N] и number[N] требуемым образом. Проверять, является ли вершина точкой сочленения, можно на шаге 3a. Также, если реализовать стек для хранения ребер, можно реализовать вывод самих двусвязных компонент: ребро нужно добавлять в стек на шагах 3a (перед рекурсивным вызовом) и 3b и выталкивать из стека в поток вывода все ребра вплоть до текущего (curr, i), если на шаге 3а выяснилось, что для текущей вершины curr выполняется условие теоремы

26) В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная или косвенная рекурсия), например, функция   вызывает функцию  , а функция   — функцию  . Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

29) Алгоритм с возвратом

Try(int i) {

инициализация выбора хода; do

выбор очередного хода из списка возможных; if (выбранный ход приемлем) { запись хода; if (доска нe заполнена) {

Try(i+1); if(неудача)

отменить предыдущий ход;

} }

while(неудача) && (есть другие ходы); }

Для более детального описания алгоритма нужно выбрать

некоторое представление для данных. Доску можно

представлять как матрицу h:

h [х, у] = 0 – поле (х, у) еще не посещалось

h [х, у] = i – поле (х, у) посещалось на i-м ходу

Выбор параметров Параметры должны определять начальные условия следующего хода

и результат (если ход сделан). В первом случае достаточно задавать

координаты поля (х, у), откуда следует ход, и число i, указывающее

номер хода.

Очевидно, условие «доска не заполнена» можно переписать как

i < п².

Кроме того, если ввести две локальные переменные u и v для позиции

возможного хода, определяемого в соответствии с правилами хода

коня, то условие «ход приемлем» можно представить как

конъюнкцию условий, что новое поле находится в пределах доски

(l≤ u ≤ n && 1 ≤ v ≤ n) и еще не посещалось

h[u,v] == 0.

Отмена хода: h[u,v] = 0.

30) (n – количество шагов, m – количество вариантов на каждом шаге)

Try(int i)

{

int k;

for (k=1; k<= m; k++)

{

выбор k-го кандидата; if (подходит)

{ его запись; if (i < n) Try(i+1); else печатать решение;

стирание записи ;

}

}

}

32) Имеются два непересекающихся множества А и В. Нужно найти

множество пар <а, Ь>, таких, что а Î A, b ÎВ, и они удовлетворяют

некоторым условиям.

Для выбора таких пар существует много различных критериев;

один из них называется «правилом стабильных браков».

Пусть А — множество мужчин, а В — женщин. У каждых мужчины и

женщины есть различные предпочтения возможного партнера.

Если среди n выбранных пар существуют мужчины и женщины, не

состоящие между собой в браке, но предпочитающие друг друга, а не

своих фактических супругов, то такое множество браков считается

нестабильным. Если же таких пар нет, то множество считается

стабильным.

Алгоритм поиска супруги для мужчины m

Поиск ведется в порядке списка предпочтений именно этого

мужчины.

Try(m) {

int r; for (r=0; r<n; r++) { выбор r-ой претендентки для m; if (подходит) {

запись брака; if (m - нe последний) Try(m+1); else записать стабильное множество;

} отменить брак;

}

}

Будем использовать две матрицы, задающие предпочтительных

партнеров для мужчин и женщин: Lady и Man.

ForMan [m, r] — женщина, стоящая на r-м месте в списке для

мужчины m.

ForLady [w, r] — мужчина, стоящий на r-м месте в списке

женщины w.

Результат — массив женщин х, где х[m] соответствует партнерше

для мужчины m.

Для поддержания симметрии между мужчинами и женщинами и

для эффективности алгоритма будем использовать дополнительный

массив у: y[w] — партнер для женщины w.

31) Нахождение оптимальной выборки (задача о рюкзаке)

Пусть дано множество вещей {x₁, x₂, x₃, …x_n}.

Каждая i-я вещь имеет свой вес w_i, и свою стоимость s_i.

Нужно из этого множества выбрать такой набор вещей, что их общий вес не превышал бы заданного числа K, а их общая стоимость была бы максимальной.

Try(int i)

{