3.Типы случайных величин. Примеры.

СВ бывают:

1.дискретные (СВ принимающие отдельные друг от друга значения с определ-ми вероятностями. Пр: число успешно сданных экзаменов, число бракованных деталей)

2.непрерывные (СВ, возможные значения которых непрерывно заполняют некоторый, конечный или бесконечный, промежуток числ-й оси. Пр: время простоя вагона, масса израсход в теч-е суток топлива).

4.Дискретная случайная величина. Как можно задать закон распределения дискретной случайной величины?

Дискретные-СВ принимающие отдельные друг от друга значения с определенными вероятностями. Пр: число успешно сданных экзаменов, число бракованных деталей.

Закон распределения СВ ξ (кси) наз-ся дискретным, если существует конечное или счетное значение множеств x₁;x₂…x_к таких, что Р{ξ= x_k}= P_k; P_k≥0; ∑P_k=1. СВ имеющая дискретный закон распр-я наз-ся дискретной СВ. Ряд распред-я-это таблица, в первой строке которой указаны возможные значения СВ, а во второй соответствующие им вероятности. CD имеющая дискретный закон распр-я наз-ся дискретной СВ.

5.Непрерывная случайная величина. Что называется плотностью распределения вероятностей?

СВ ξ наз-ся непрерывной, если ее ф-ция распределения непрерывна в любой точке и дифференцируема всюду, кроме может быть определенных точек. Плотностью распр-я вероятностей непрерывной СВ в точке x называется производная ее функции распределения в этой точке: f(x)=F’(x).

6.Взаимосвязь между функцией распределения и плотностью распределения.

Ф-ция плотности распределения f(x), как и ф-ция распред-я F(x), явл-ся одной из форм задания закона распределения, но она применима только для непрерывных СВ. Ф-цию плотности распределения вероятностей f(x) еще называют дифференциальной ф-цией распределения, тогда как ф-цию распределения F(x) называют, соответственно, интегральной ф-цией распределения.

7.Свойства плотности распределения.

1) Плотность распределения вероятностей – неотрицательная функция: f(x)≥0; (геометрически: кривая распределения лежит не ниже оси абсцисс).

2) Вероятность попадания значения случайной величины на участок от  до  определяется по формуле: P(α<X<β)=_α^β∫f(x)dx;

3) Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом:

F(x)=P(X<x)=P(-∞<X<x)=^x_-∞∫f(t)dt;

4)^∞_-∞∫f(x)dx=1, (^b_a∫f(x)dx=1)

8.Числовые характеристики распределения случайной величины.

Числ-е характеристики-числа, описывающие некоторые характерные черты, распределение. (матем-ое ожидание, мода, медиана, дисперсия, коэффициент асимметрии, коэффициент эксцесса)

9.Математическое ожидание случайной величины, ее свойства.

Математическое ожидание характеризует среднее значение случайной величины, вокруг которого группируются все ее значения. Термин «математическое ожидание» связан с начальным периодом развития теории вероятностей, когда она развивалась на примерах и задачах азартных игр и игрока интересовал средний выигрыш, то есть среднее значение ожидаемого выигрыша. Для дискретных и непрерывных случайных величин математическое ожидание вычисляется, соответственно, по формулам (17) и (18) (при условии, что ряд в формуле (17) и интеграл в формуле (18) сходятся абсолютно):

; (17)

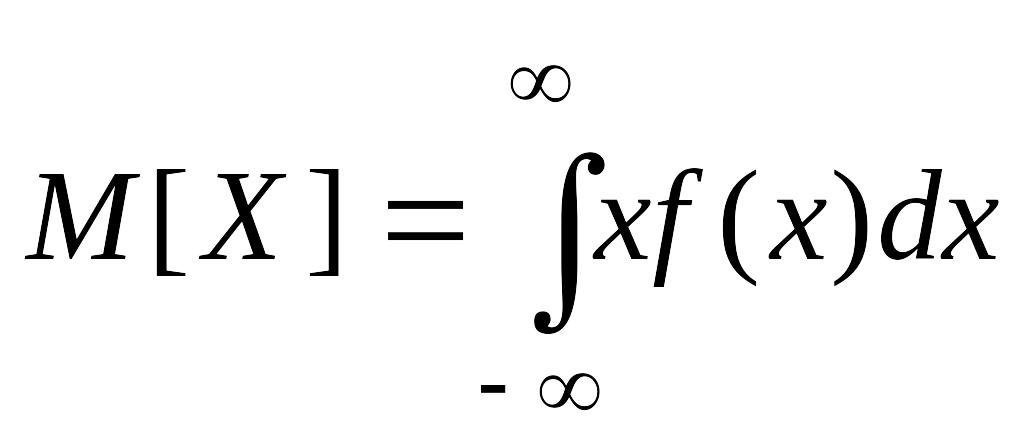. (18)

В механической интерпретации математическое ожидание характеризует центр тяжести системы.

Свойства математического ожидания:

а) математическое ожидание постоянной величины равно этой постоянной:

M[C] = C;

б) постоянный множитель можно выносить за знак математического ожидания:

M[CX] = C M[X];

в) математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий.

г) если , то M[X] , то есть математическое ожидание произвольной случайной величины X принадлежит интервалу между минимальным и максимальным возможными значениями случайной величины X;

д) математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий.