21. Схема испытаний Бернулли.
Построим математ. Модель независимых экспериментов, повторяющихся при неизменных условиях. При чем:
1)Число экспериментов п – конечно.
2)В каждом эксперименте мы наблюдаем 2 события А и А(против.) (успех и неудача)
3) Все эксперименты независимы друг от друга.
4) Вероятность наступления соб. А постоянна и равна Р для каждого эксперимента соответственно вероятность наступления А(против) в каждом экспер. Так же постоянна и равна q=1-p.
22. Формула Бернулли. Наиболее вероятное число наступления «успехов» в схеме.
Р(В)=Рn(m)=Вероятность того, что в п испытаний успех наступит ровно m раз.
np-q<=mo<=np+p
1) np-q – целое, то существует 2 наивероятн. Числа mo, mo+1.
2) если np-q –дробное, то существует 1 наивер. Число наступления «успеха».
3) Если n*p – целое, то существует 1 число, оно равно mo=n*p.
23. Локальная теорема Муавра-Лапласа
Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний ровно m раз приближенно равна (тем точнее, чем больше n) значению функции
,
.
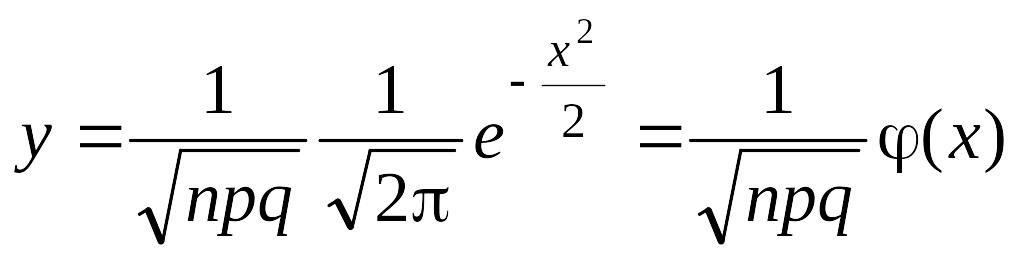Функция
(x)
является четной функцией, то есть
(– x) = (x),
для всех
принимается ( x) = 0.
Таким образом, вероятность того, что
событие A
появится в n
независимых испытаниях ровно m
раз, приближенно равна
,
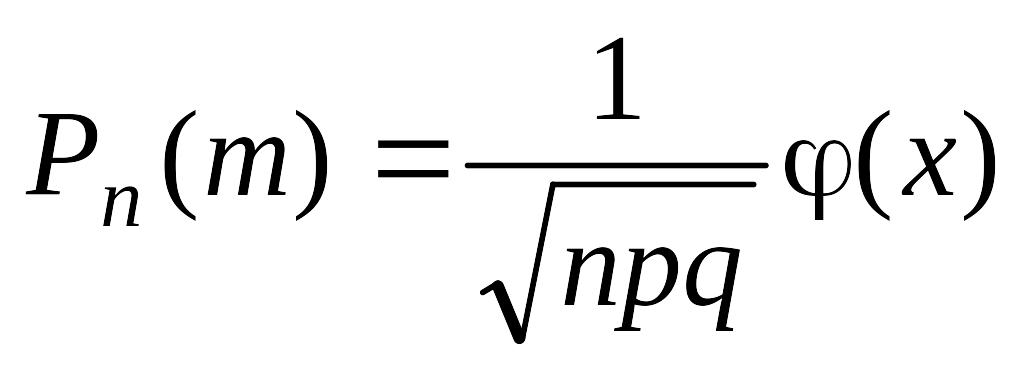где
.
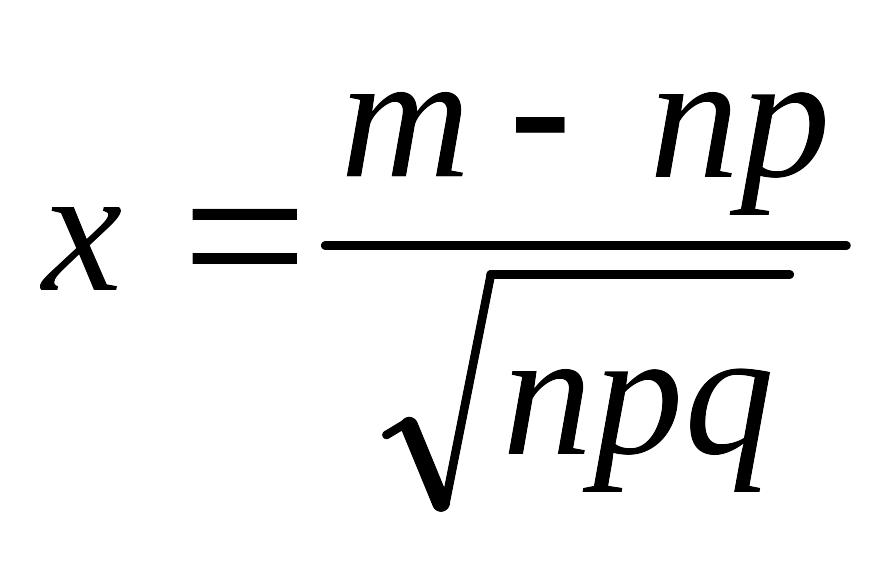24. Интегральная теорема Муавра-Лапласа
Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний от k1 до k2 раз, приближенно равна
,
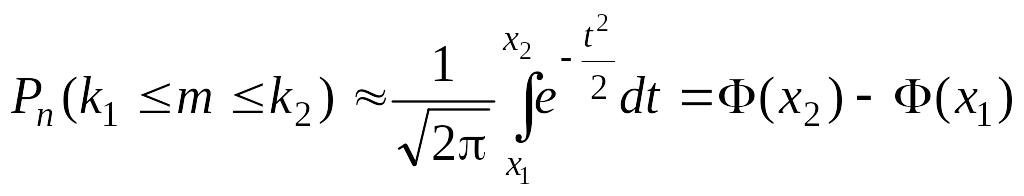где
,
.
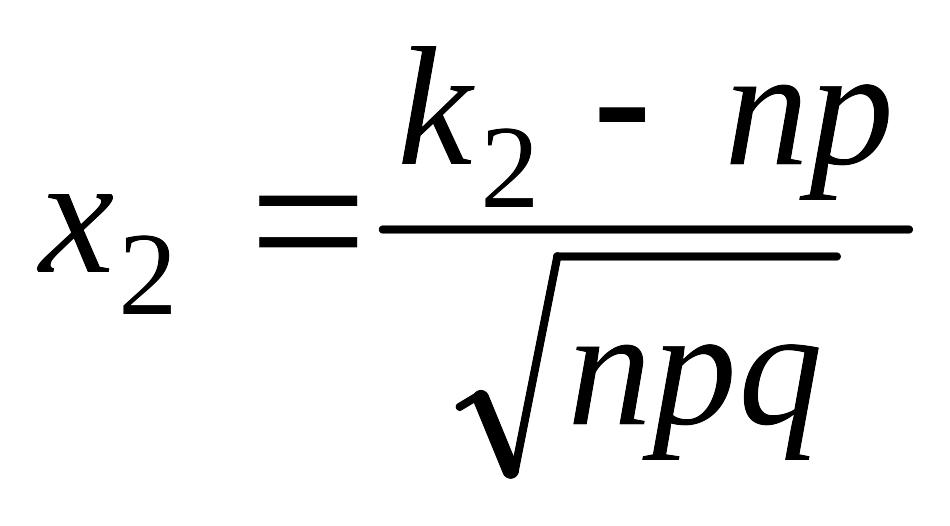Функция (x) нечетна, то есть (– x) = – (x). При x > 5 можно принять (x) = 0,5.
25. Теорема Пуассона
Пусть
число экспериментов Бернулли велико
(
),
а вероятность наступления события A
в каждом испытании очень мала (
),
тогда вероятность того, что событие A
появится в серии из n
испытаний ровно m
раз, приближенно равна
где
произведение
.
|
2 Раздел.
1.Определение случайной величины, типы случайных величин, примеры. Закон распределения вероятностей случайной величины.
СВ-величина, значения которой зависят от случая и для которой определена функция распределения вероятностей. СВ бывают дискретные (СВ принимающие отдельные друг от друга значения с определ-ми вероятностями. Пр: число успешно сданных экзаменов, число бракованных деталей), непрерывные (СВ, возможные значения которых непрерывно заполняют некоторый, конечный или бесконечный, промежуток числ-й оси. Пр: время простоя вагона, масса израсход в теч-е суток топлива). Закон распред-я СВ-любое правило, позволяющее находить вероятности всевозможных событий связанных со СВ.
2.Фукция распределения вероятностей случайных величин, ее свойства.
Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть F(x) = P(X < x).
Основные свойства функции распределения F(x):
1 Так как по определению F(x) равна вероятности события, все возможные значения функции распределения принадлежат отрезку [0; 1]:
0 F(x) 1.
2 Если
,
то
,
то есть F(x) –
неубывающая функция своего аргумента.
3 Вероятность того, что случайная величина примет значение, принадлежащее полуинтервалу [a, b), равна приращению функции распределения на этом интервале:
P(a X < b) = F(b) – F(a).
4 Если все возможные значения случайной величины принадлежат отрезку [a, b], то
F(x) = 0, при x a; F(x) = 1, при x > b.
Функция распределения дискретных случайных величин может быть определена по формуле:
.
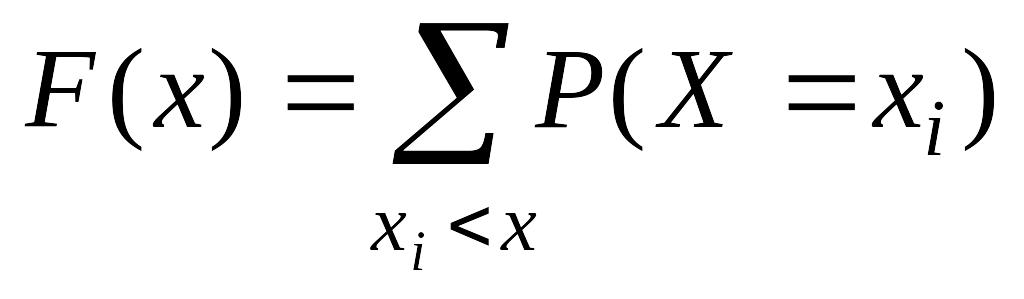Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения.