17. Теоремы умножения вероятностей (для двух и для трёх событий). Условия их применения.

Теорема1: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло, т.е.. Р(А∩В)=Р(А)*Р(В| А)

Теорема2: Вероятность произведения двух независимых событий А и В равна произведению их вероятностей Р(А∩В)=Р(А)*Р(В)

Для 3-х событий - Р(А∩В∩С)=Р(А)*Р(В|А)*Р(С| А∩В)

18. Теоремы сложения вероятностей (для двух и для трёх событий). Условия их применения.

Теорема1: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Теорема2: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ).

Для 3-х событий - Р (АỦВỦС)=Р(А)+Р(В)+Р(С)-Р(А∩В)-Р(В∩С)-Р(А∩С)+ Р(А∩В∩С)

19. Формула полной вероятности.

Частным случаем применения теорем сложения и умножения вероятностей является формула полной вероятности. При решении многих практических задач часто встречаются с ситуацией, когда прямое вычисление вероятности события A трудно или невозможно, в то время как вполне доступно определение вероятности этого события при некоторых различных условиях H_i.

Условия применения формулы полной вероятности :

Пусть производится испытание, об условиях которого можно сделать n взаимно исключающих предположений: H₁, H₂,…, H_n (H_i  H_j = , при i  j), таких, что

H₁+ H₂+…+ H_n = .

Поскольку заранее неизвестно, какое из событий H_i произойдет, эти события называют гипотезами. Предполагается, что вероятности гипотез известны и равны соответственно P(H₁), P(H₂),…, P(H_n). Так как события H₁, H₂,…, H_n несовместны и образуют полную группу событий, то P(H₁)+ + P(H₂)+…+P(H_n) = 1.

Тогда любое рассматриваемое событие A может произойти только одновременно с осуществлением одной из гипотез H₁, H₂,…, H_n. То есть A = A  H₁  A  H₂  …  A  H_n. Поскольку события A  H₁, A  H₂,…, A  H_n – несовместны, P(A) = P(A  H₁) + P(A  H₂) + … + P(A  H_n). Применив теорему умножения вероятностей, можно записать: P(A  H_i) = P(H_i)P(A|H_i).

Таким образом, приходим к формуле полной вероятности, позволяющей определить «полную» вероятность события A через известные условные вероятности события A при гипотезах H_i:

P(A) = P(H₁)P(A|H₁) + P(H₂)P(A|H₂) + … + P(H_n)P(A|H_n)= .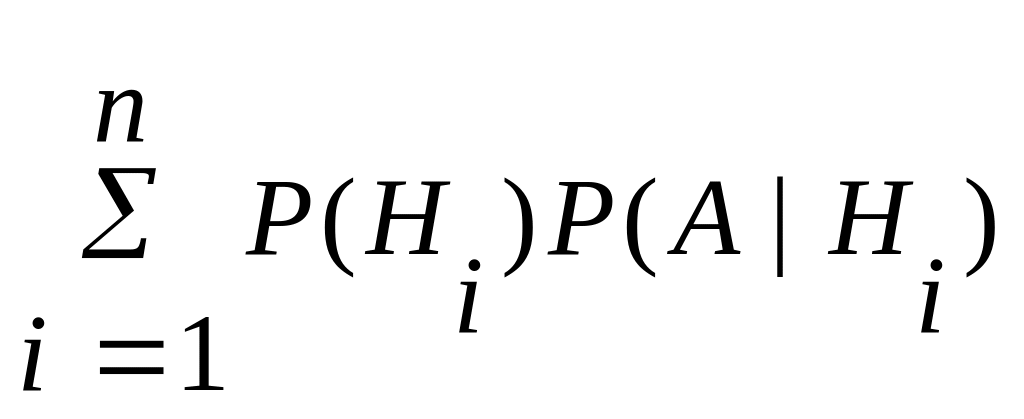

20. Формула Байеса.

Частным случаем применения теорем сложения и умножения вероятностей является формула Байеса. При решении многих практических задач часто встречаются с ситуацией, когда прямое вычисление вероятности события A трудно или невозможно, в то время как вполне доступно определение вероятности этого события при некоторых различных условиях H_i.

Сформулируем условия применения формулы Байеса.

Если известно, что в результате опыта произошло событие A, то новые, апостериорные (послеопытные) вероятности гипотез можно определить по формуле Байеса

= .

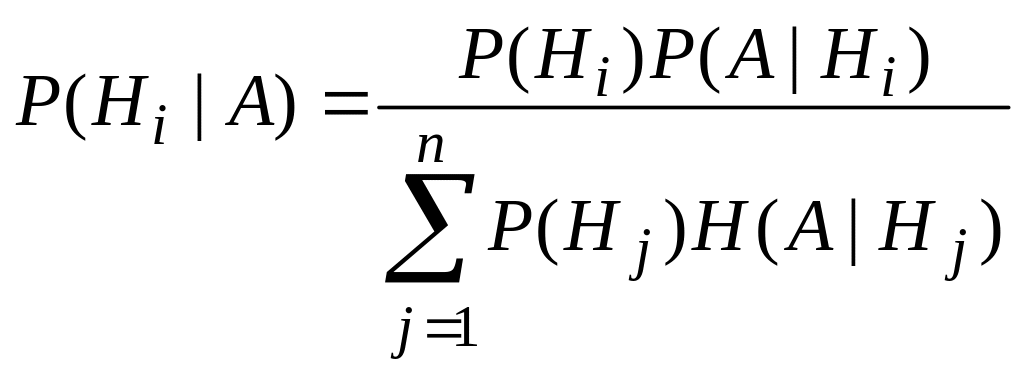Эти вероятности, которые интересуют нас после проведения эксперимента, называются апостериорными вероятностями. Вероятности гипотез P(H_i), которыми мы должны располагать до проведения эксперимента, называются априорными вероятностями.

Таким образом, формула Байеса – это формула пересчета вероятностей гипотез на основании результатов эксперимента. Легко видеть, что сумма апостериорных вероятностей гипотез равна единице.