12. Статистический метод вычисления вероятности.

Существует большой класс событий, вероятности которых нельзя вычислить с помощью классического метода определения вероятностей. Например: - выпадение некоторой грани игральной кости со смещенным центром тяжести, - попадание в цель при одном выстреле, - выход из строя прибора в течение гарантийного срока и т.д.

Можно предположить, что каждое из таких событий обладает некоторой вероятностью, которая при многократном повторении соответствующих опытов будет отражаться в относительной частоте событий. Относительной частотой события А в некоторой серии из N испытаний называется отношение числа испытаний N_А, в которых событие А произошло, к общему числу произведенных испытаний N.

Экспериментальным фактом является то, что при неограниченном увеличении числа испытаний относительная частота события А приближается к вероятности события А и стабилизируется около этого значения.

При статистическом определения вероятности в качестве вероятности события используется относительная частота этого события в большой серии испытаний.

13. Аксиоматический метод задания вероятности.

Пусть проводится вероятностный эксперимент Е и Ώ – дискретное пространство этого эксперимента.

Теорема. Если в дискретном пространстве Ώ содержащем конечное или счетное множество элементарных исходов задана вероятностная мера.

Р = { p(ώ 1), p(ώ 2)…p(ώ n)}, P(ώi) =>0, Σ P(ώi) =1, то вероятность появления произвольного события А

А = { ώА1, ώA2… ώAn} равна Р(А) = Σ Р(Ааi).

Доказательство следует из 3-ей аксиомы Колмогорова.

14. Свойства вероятностей.

Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда:

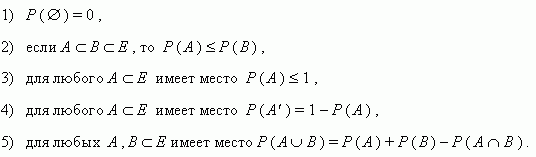
15. Условные вероятности. Аксиомы Колмогорова (для случая условных вероятностей).

Условной вероятностью события A при условии B (обозначается P(A|B)) называется вероятность события A, вычисленная при условии, что событие B произошло. По определению

P(A | B) = P(A  B)/P(B).

Вычисление условных вероятностей – это, по существу, переход в новое, урезанное заданным условием B пространство элементарных событий. Вероятности элементарных событий P(_i) (_iB) пропорциональны исходным. Для соблюдения условия нормировки в новом пространстве элементарных событий они делятся на P(B).

Аналогично

P(B | A) = P(A  B)/P(A)

в случае, если P(A)  0.

16. Независимость событий (для двух и для трёх событий).

С понятием условной вероятности тесно связано понятие независимости событий.

Понятие независимости можно перевести на язык математики:

Е….где (Ώ, А, Р) – матем. Модель этого эксперимента.

Говорят, что событие А не зависит от события В, если наступление события В не изменяет вероятности наступления события А.

Т.е. p (A | B)=Р(А).

Если p (A | B)не равно Р(А)., то событие А называется зависимым от события В.

Р(А∩В)=Р(А)*Р(В) – теорема умножения независимых событий.

Понятие независимости можно распространить на случай 3-х и более событий.

События А, В, С называются попарно независимыми если выполняются следующие равенства.

Р(А∩В)=Р(А)*Р(В)

Р(А∩С=Р(А)*Р(С)

Р(В∩С)=Р(В)*Р(С).

События А, В, С независимы в совокупности если выполняются следующие равенства

Р(А∩В)=Р(А)*Р(В)

Р(А∩С=Р(А)*Р(С)

Р(В∩С)=Р(В)*Р(С).

Р(А∩В∩С)=Р(А)*Р(В)*Р(С)

Теорема. Если 2 события А и В наблюдаются в 1-ом эксперименте, то независимы также А и В(против), А(против) и В, А(против) и В(против).

Это означает, что

p (A | B)=Р(А)

p (В | А)=Р(В)

Р(А∩В)=Р(А)*Р(В) – независимы

Р(А∩В)=Р(А)*Р(В| А)= Р(В)* p (A | B) – зависимы.