16. Доверительные Интервалы для математического ожидания нормально распределенной случайной величины

Пусть вероятностный эксперимент описывается случайной величиной X и известно, что X подчиняется нормальному закону распределения вероятностей.

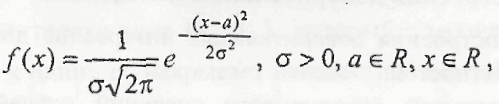
где σ - среднее квадратическое отклонение случайной величины X, причем значения σ и а нам неизвестны;

а - математическое ожидание.Построим доверительный интервал для неизвестного значения а математического ожидания.

Найдём оценки параметров

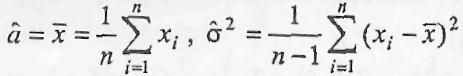
Составим вспомогательную величину

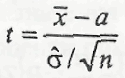
Случайная величина t распределена по коэффициенту Стьюдента

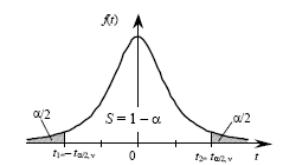
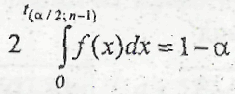
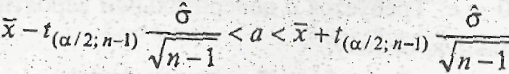
17. Функциональная, статистическая, регрессионная зависимость.

Зависимость между случайными величинами, при которой каждому значению х случайной величины Х однозначно ставится в соответствие единственное значение у с.в. У, называется функциональной.

Однако часто на практике 1-ому значению с.в. Х может соответствовать не одно, а множество значений с.в. У, характеризуемых для каждого Х=х условным распределением м плотностью вероятностей f(y│X=x).

Такая зависимость называется статистической.

Регрессионная зависимость – каждому значению одной с.в. ставит в соответствие условное математическое ожидание другой с.в. M[Y│X=x]

18. Корреляционное поле. Выбор модели регрессионной зависимости.

Пусть дана выборка значений двумерной св. (X,Y)=:{(x1,у1), (х2,У2) ... [хп,Уп)}\ где п - объем двумерной выборки. Первым шагом в построении эмпирического уравнения регрессии между с. в. является графическое отображение значений двумерной с. в. в виде точек (х1, у1),..., (хл,уп) на плоскости Х- Y, называемое диаграммой рассеяния (корреляционным полем).

Визуальный анализ диаграммы рассеяния и предметная постановка задачи (физический смысл рассматриваемых величин) позволяет сделать предположение о виде уравнения регрессии. Если предполагается, что зависимость между с.в.Хи У линейна, то теоретическая модель регрессионной зависимости между св. задается уравнением теоретической моделью линейной регрессии У на Х:

Т.е для каждого Х=хi имеется условное распределение с.с У со средним значением (β0+ β1хi). Таким образом для каждого i-того наблюдения справедлива след. Зависимость:

Где уi - выборочное значение с. в. У;

βо - параметр линейной регрессии, требующий определения;

β 1- параметр линейной регрессии, требующий определения;

хi - выборочное значение с. в. X;

ei- ошибка, вызванная отклонением i-го наблюдения с. в. У от условного среднего M[Y\X=xi].

20.Коэффициент корреляции, его свойства.

Основной числовой характеристикой ,определяющей тесноту линейной связи между двумя случайными величинами, является коэффициент корреляции

Известны следующие свойства коэффициента корреляции r:

1 Возможные значения коэффициента корреляции принадлежат отрезку

[-1, 1]: -1 ≤r ≤ 1

2 Необходимым и достаточным условием отсутствия линейной зависимости между исследуемыми величинами является равенство нулю соответствующего коэффициента корреляции.

3 Если корреляция между переменными Х и Y положительна (то есть, если при увеличении значений одной переменной, значения другой также

имеют тенденцию к возрастанию), то r > 0; если имеет место отрицательная корреляция (при увеличении значений одной переменной значения другой, в

среднем, убывают), то r < 0.

4 Чем ближе по модулю значение коэффициента корреляции к единице, тем теснее линейная зависимость между изучаемыми величинами.

5 │r=1│ тогда и только тогда, когда между переменными Х и Y существует линейная функциональная зависимость.

6 Значение коэффициента корреляции не зависит от выбора начала отсчета и единиц измерения исследуемых величин.