14.Коэффициент эксцесса.

Коэффициент эксцесса (обозначается Ex[X]) характеризует островершинность графика функции плотности распределения вероятностей f(x). Своеобразным началом отсчета при измерении степени островершинности служит нормальное распределение, для которого Ex[X] = 0. Как правило, распределения с более высокой и более острой вершиной кривой плотности распределения (или многоугольника распределения) имеют положительное значение коэффициента эксцесса, а с более низкой и пологой – отрицательное значение.

Для вычисления значений коэффициента эксцесса дискретных и непрерывных случайных величин используются следующие формулы:

; .

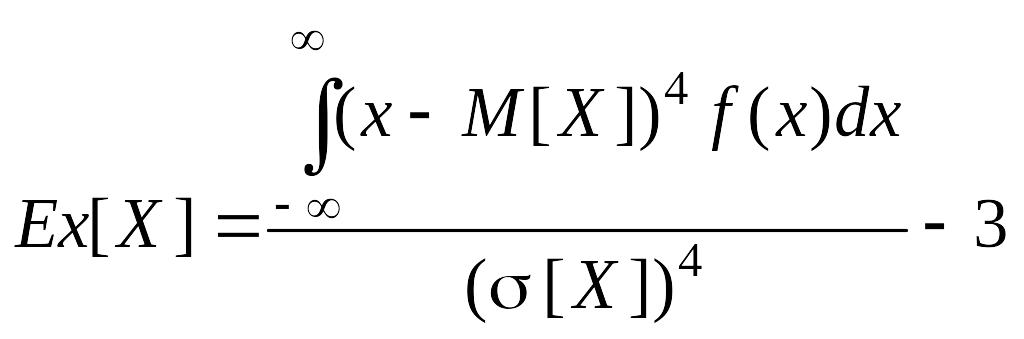15.Закон распределение вероятностей Пуассона.

Говорят, что дискретная СВ ξ (кси) имеет распределение Пуассона, если ее возможные значения 0,1,2,…,m…, а вероятность вычисляется по формуле: Р(ξ=m)=(a^m/m!)e^-a , где

1. параметр распределения.

16.Равномерный закон распределения случайной величины.

Говорят, что СВ ξ имеет равномерное распределение на интервале (а,b), если функция ее плотности равна: f(x)=система: 1/(b-a), x€(a,b); 0, x€(a,b)

17.Показательный закон распределения случайной величины.

Говорят, что непрерыв СВ ξ имеет показательное распределение, если функция ее плотности имеет вид: f(x)=система: λe^-λx, x≥0; 0, x<0, λ-параметр

18.Нормальный закон распределения случайной величины.

Говорят, что непрерыв СВ ξ подчиняется нормальному закону распределения, если плотность распределения имеет вид: f(x)=(1/δ√2π)е^{-((x-a)^2/2δ^2)}, P{α≤ξ≤β}=Ф((β-а)/δ)-Ф((α-а)/δ)

19.Функция Лапласа, ее график и свойства.

Как известно, неопределенный интеграл не выражается через элементарные функции, но его можно выразить через специальную функцию

,

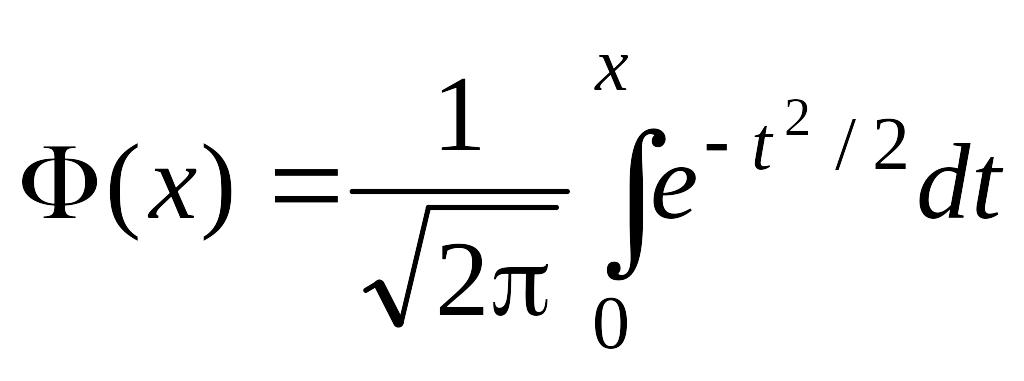называемую функцией Лапласа (или «интегралом вероятностей»), для которой составлены таблицы значений. В геометрической интерпретации Ф(x) равна площади фигуры под кривой (x), опирающейся на отрезок [0; x].

Функция (x) – нечетная, то есть (– x) = – (x); при x > 5 можно принять (x) = 0,5.

С помощью функции Лапласа вероятность попадания нормально распределенной случайной величины X на участок от  до  выражается формулой

.

Формула для расчета вероятности отклонения нормально распределенной случайной величины Х от своего математического ожидания на величину имеет вид:

.

20.Функция плотности стандартного нормального распределения, ее график и свойства.

Свойства

21.Функция распределения дискретной случайной величины.

Функция распределения дискретной случайной величины может быть определена по формуле F(x)=_xi<x∑P(X=x_i)

22.Функция распределения непрерывной случайной величины.

Функция распределения непрерывной СВ предст. собой ф-ию, непрерывную во всех точках.

Из непрерывности ф-ии F(x) следует, что вероятность каждого отдельного значения непрерывной СВ равна нулю.

Так как вероятность каждого отдельного значения непрерывной СВ равна 0, св-во ф-ии распределения для непрерывной СВ будет иметь вид

P( ) = P( ) = P( ) = P( ) = F(b) – F(a)

23.Вероятность попадания значений дискретной случайной величины в интервал [α,β].

Вероятность попадания СВ на заданный участок равна приращению ф-ии распределения на этом участке. Если неограниченно уменьшать участок ( ), то . В пределе вместо вероятности попадания на участок получится вероятность того, что величина примет отдельно взятое значение

Если в точке ф-ия F(x) имеет разрыв, то предел равен значению скачка ф-ии F(x) в точке

24.Вероятность попадания значений непрерывной случайной величины в интервал [α,β].

Вероятность попадания СВ на заданный участок равна приращению ф-ии распределения на этом участке. Если неограниченно уменьшать участок ( ), то . В пределе вместо вероятности попадания на участок получится вероятность того, что величина примет отдельно взятое значение

Если в точке ф-ия F(x) непрерывна, то этот предел равен нулю.

25.Графическое изображение законов распределения дискретной и непрерывной случайной величины.

3 РАЗДЕЛ.

1. Что называется выборкой и генеральной совокупностью? Требования, которые должна удовлетворять выборка.

Множество всех значений {х1,х2…хn}называется выборкой значений случайной величины.

Выборка, результат огранич. ряда наблюдений случ. величины.

Мн-во всех мыслимых наблюдений, которые могли бы быть зафиксированы при воспроизведение эксперимента ,принято называть генеральной совокупностью.

Требования, которые должна удовлетворять выборка:

1.выборка {х1,х2…хn}наз-ся представительной, если каждый элемент совокупности имеет одну и ту же вероятность включения в выборку

2.выборка {х1,х2…хn}должна быть получена в рез-те проведения n-независимых испытаний, а все элементы выборки должны принадлежать одной и той же случ. величине.