13. Приложения векторного произведения двух векторов.

Учитывая свойство векторного произведения, что , а произведение разных базисных векторов, есть третий базисный вектор со знаком + или -, чтобы не ошибиться со знаком, удобно пользоваться следующей схемой:

+

Векторное произведение двух последующих стоящих, равно следующему за ними вектором, при этом, если движение осуществляется слева направо = , справа налево = .

Векторное произведение 2-х векторов, так же как и скалярное произведение, имеет определенный физический смысл.

Пусть на материальную точку М, действует сила и задана точка А. Тогда векторное произведение определяет момент силы относительно точки А, тоесть .

1. Берем две точки и делаем из них вектор.

2. Вычисляем по формуле.

Векторное произведение двух векторов имеет и определенный геометрический смысл. По определению векторного произведения , , модуль векторного произведения, равен площади параллелограмма, построенного из .

Соответственно построенного на будет .

.

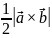14. Смешанное произведение трех векторов. Свойства.

Смешанным произведением 3-х векторов называется число равное скалярному произведению векторного произведения векторов на вектор . .

Свойства:

1. Смешанное произведение не меняется при перестановке знаков скалярного и векторного умножения.

Это позволяет записывать смешанное произведение в виде .

2. Смешанное произведение меняет знак при перемене мест, любых двух векторов сомножителей.

3.

4.

5. Если смешанное произведение 3-х ненулевых векторов , значит векторы компланарные. Справедливо и обратное утверждение, если векторы компланарные, то их смешанное произведение равно 0.

Отсюда следует, что смешанное произведение 3-х векторов, из которых 2-е коллинеарные, равно 0.

15. Приложения смешанного произведения трех векторов.

Смешанное произведение 3-х векторов имеет определенный геометрический смысл.

Объем параллелепипеда построенного на векторах равен модулю смешанного произведения этих векторов.

Соответственно, объем треугольной пирамиды построенной на векторах , будет равен:

Помимо нахождения объемов тел, смешанное произведение 3-х векторов применяется для установления комапланарности векторов и определения взаимной ориентации векторов в пространстве.

Если смешанное произведение равно 0, то векторы компланарные, если смешанное произведения > 0, то векторы образуют правую 3-ку, если < 0 – левую тройку.

16. Вычисление скалярного, векторного и смешанного произведения векторов в ортонормированном базисе.

Скалярное произведение:

Векторное произведение:

Смешанное произведение:

4. Линейные пространства

1. Линейное пространство.

Множество L элементов любой природы, называется линейным пространством, если:

1. На множестве L определена операция сложения, которая любым двум элементам из множества L, ставит в соответствие элемент принадлежащий множеству L, который обозначает , и называется их суммой.

2. На множестве L, определена операция умножения на действительное число, которая каждому элементу , и каждому действительному числу , ставит в соответствие элемент принадлежащий множеству L, обозначаемый , и называемый произведением на .

3. Данные операции удовлетворяют следующим аксиомам:

1. , для любых из множества L.

2. , для любых из множества L.

3. Во множестве L, существуют нулевой элемент – 0, такой, что , для любого элемента из множества L.

4. Для каждого элемента из множества L, существует противоположный элемент , принадлежащий множеству L, такой, что .

5. , для каждого из множества L, и любых чисел .

6. , для любых из множества L и любого числа L.

7. , для всякого из множества L, и любых чисел

8. , для всякого ненулевого из множества L.

2. N-мерный вектор. Линейные операции над N-мерными векторами. Линейное арифметическое пространство.

Рассмотрим множество упорядоченных наборов из n-действительных чисел. Записываем их в виде 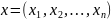. Элементы данного множества называются n-мерными векторами. Данное название обусловлено тем, что при , набор чисел можно интерпретировать как совокупность координат вектора на плоскости (в пространстве).

Операция сложения элементов:

Легко показать, что данные операции над n-мерными векторами, удовлетворяют всем требованиям линейного пространства, следовательно, множество n-мерных векторов, с данными операциями сложение элементов и умножение элементов на число, является линейным пространством. Оно называется арифметическим пространством, и обозначается .