6. Аналитическая геометрия в пространстве

1. Уравнение плоскости: каноническое, общее, в отрезках. Основные способы составления уравнения плоскости (через три точки, через точку и нормальный вектор).

– Общее уравнение плоскости.

– Каноническое уравнение плоскости.

Способы составления плоскости:

1. Через три точки:

2. Через точку и нормальный вектор (только при пендикулярности):

2. Вывод формулы расстояния от точки до плоскости.

d – расстояние от до плоскости , равно модулю проекции вектора на направление нормального вектора плоскости, где произвольная точка плоскости. Следовательно,

Так как точка принадлежит плоскости, то , откуда следует, что .

Таким образом расстояние d от т.М до плоскости

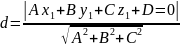
3. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.

Из условий коллинеарности и перпендикулярности векторов, следуют условия параллельности и перпендикулярности плоскостей.

Плоскости параллельны тогда и только тогда, когда нормальные векторы и коллинеарны (пропорциональные координаты). Делим их а б ц. И если норм, то норм.

Плоскости перпендикулярны только когда скалярное произведение нормальных векторов и плоскостей равно 0.

4. Параметрические, канонические, общие уравнения прямой линии в пространстве. Какие уравнения приводятся к каноническим.

или – Параметрические уравнения прямой.

– Канонические уравнения прямой.

– Общие уравнения прямой в пространстве

Для перехода общих уравнений к каноническим необходимо найти точку на прямой, и направляющий вектор . Координаты , находим как частное решение системы уравнений .

Для этого, одной из неизвестных, придают произвольное значение (например z=0).

Решая полученную систему, находим две координаты точки.

Направляющий вектор прямой, параллельной линии пересечения плоскостей, и следовательно перпендикулярен нормальным векторам и , поэтому в качестве направляющего вектора прямой берем .

Координаты какой либо точки найдем, придав z нулевое значение (z=0).

Направляющий вектор прямой, находим как векторное произведение нормальных векторов и плоскостей.

Вычисляем и ж к, и записываем это вниз, а частное вверх.

Бинго.

5. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности.

Где, направляющие векторы.

Из условий коллинеарности и перпендикулярности векторов, следующих условий параллельности и перпендикулярности прямых в пространстве.

Прямые параллельны тогда и только тогда, когда направляющие вектора прямых коллинеарны. Делим их м н п.

Прямые перпендикулярны тогда и только тогда, когда скалярное произведение направляющих векторов

6. Взаимное расположение двух прямых линий в пространстве.

Две прямые (канонические).

Прямые располагаются в одной плоскости тогда и только тогда, когда векторы , компланарные, то есть смешанное произведение = 0.

Следовательно условием принадлежности двух прямых одной плоскости является равенство (определитель 3-го порядка = 0, первая строка , вторая , третья ).

При этом если направляющие векторы неколлинеарны, то прямые пересекаются, если коллинеарные, то прямые параллельны (а если все три вектора, то прямые совпадают).

Если условие принадлежности двух прямых одной плоскости не выполняется, то прямые являются скрещивающимися.