- •1.Понятие дифференциального уравнения, его порядка и решения.
- •2.Оду первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения. Постановка задачи Коши.
- •3.Формулировка теоремы существования и единственности ( тсе ). Понятие общего решения.
- •4.Уравнения с разделяющимися переменными. Однородные уравнения. Примеры.
- •5.Линейные уравнения первого порядка. Уравнения Бернулли.
- •6.Обобщенное понятие интегральной кривой.
- •7.Уравнения первого порядка, не разрешенные относительно производной.
- •8.Общий метод введения параметра.
- •9. Уравнения Лагранжа и Клеро.
- •10. Оду порядка n: определение решения, постановка задачи Коши, формулировка тсе.
- •11.Простейшие методы понижения порядка.
- •13. Лду порядка n и линейный дифференциальный оператор. Свойство решений однородного лду.
- •14 Линейно зависимые и линейно независимые системы функций. Определитель Вронского и необходимое условие линейной зависимости произвольной системы функций.
- •15 Теорема об определителе Вронского системы линейно независимых решений однородного лду порядка п.
- •16 Теор.
- •17. Теорема об общем решении неоднородного лду порядка n.
- •18. Метод вариации произвольных постоянных для неоднородного лду порядка n
- •19. Фср однородного лду с постоянными коэффициентами в случае простых корней характеристического ур-ия(действительных или комплексных)
- •20. Фср однородного лду с постоянными коэффициентами в случае, когда характеристическое ур-ие имеет кратные корни
- •21.Отыскание частных решении неоднородного лду с постоянными коэффициентами и стандартной правой частью.
- •22. Нормальная система оду. Понятия решения и интегральной кривой.Постановка задачи Коши для нормальной системы, формулировка тсе.
- •23. Нормальная система лду. Скалярная и матричная запись. Формулировка тсе решения задачи Коши для системы лду.
- •24. Свойства решений однородной системы.
- •29. Метод вариации произвольных постоянных для неоднородной системы лду.
- •30. Фср однородной системы лду с постоянными коэффициентами с случае простых действительных корней характеристического уравнения.
- •32.Понятие устойчивости по Ляпунову и ассимптотической устойчивости. Сведение исследования устойчивости решения к исследованию устойчивости нулевого решения.
- •33. Устойчивость системы лду. Необходимое и достаточное условие устойчивости линейной системы.
- •34. Теорема об устойчивости системы лду с постоянными коэффицентами.
- •35. Понятие фазового пространства и фазовой траектории. Автономные системы оду, св-ва их фазовых траекторий.
- •36. Исследование устойчивости положения покоя системы двух лду с постоянными коэффициентами в случае , - действительные.
- •37. Исследование устойчивости положения покоя системы двух лду с постоянными коэффициентами в случае , - комплексные.
- •38. Исследование устойчивости положения покоя системы двух лду с постоянными коэффициентами в случае ,
- •39. Исследование устойчивости положения покоя системы двух лду с постоянными коэффициентами в случае .
- •40. Нелинейные системы. Исследование устойчивости по первому приближению. Теорема Ляпунова.
20. Фср однородного лду с постоянными коэффициентами в случае, когда характеристическое ур-ие имеет кратные корни
(15)
Опред.:Говорят
что число
является корнем многочлена
 кратности k,если
кратности k,если
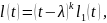 где
где
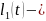 многочлен
степени(n-k),
многочлен
степени(n-k),
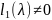 .
.
Пусть – корень кратности k:
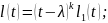
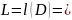 ;
;
Рассмотрим

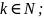
Теорема8:
Пусть
является корнем кратности k
характеристического многочлена
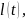 тогда функции
,
тогда функции
,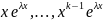 являются решением ур-ия (13).
являются решением ур-ия (13).
Док-во:
Т.к.
– корень кратности k
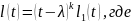
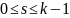
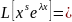
Т.е.
для
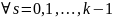 Функция
Функция
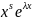 - решение ур-ия (13)
- решение ур-ия (13)
Лемма5:
Для
различных
чисел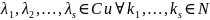
Система
функций: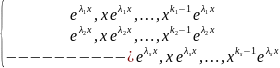
линейно
независима на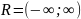
Теорема9:
Пусть
различные
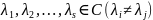 – корни характеристического многочлена
кратности
– корни характеристического многочлена
кратности
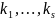 – соответственно. Тогда общее решение
ур-ия (13) имеет вид:
– соответственно. Тогда общее решение
ур-ия (13) имеет вид:
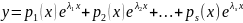 ,
где
,
где
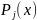 – многочлен степени
– многочлен степени
 с
произвольными комплексными коэффициентами
с
произвольными комплексными коэффициентами
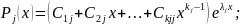 j=1…s;
j=1…s;
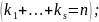
Док-во:
Т.к.
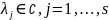 - корень характеристического многочлена
- корень характеристического многочлена
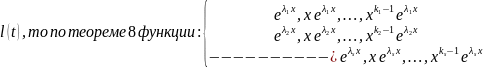
решения ур-ия (13)
Согласно
Лемме 5 эти функции линейно независимы
на
 их
их
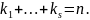 Следовательно построенная система –
ФСР ур-ия (13) и
Следовательно построенная система –
ФСР ур-ия (13) и

где
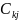 – произвольная
постоянная.
– произвольная
постоянная.
А)Действительный
случай:
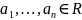
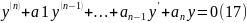
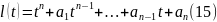
1)Пусть
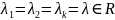 (
(
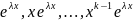 – действительные
решения
– действительные
решения
2)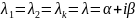
 ;
;

Комплексные функции теорема 8:
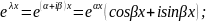
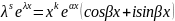 – решение
ур-ия (17)
– решение
ур-ия (17)
По
теореме: Re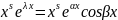
Im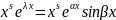 – решения ур-ия (17)
– решения ур-ия (17)
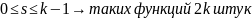
Общий
случай:
Пусть
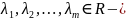 действительные
корни
для ур-ия (17) кратности
действительные
корни
для ур-ия (17) кратности
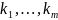 соответсвенно,
соответсвенно,
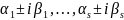 –
комплексные корни ур-ия (15) кратности
–
комплексные корни ур-ия (15) кратности
 соответственно
соответственно

Тогда общее решение ур-ия (17) имеет вид:
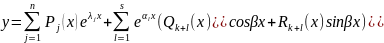
где
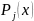 - многочлен
степени
- многочлен
степени
 – многочлены
степени
– многочлены
степени
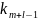 с произвольными действительными
коэффициентами.
с произвольными действительными
коэффициентами.
21.Отыскание частных решении неоднородного лду с постоянными коэффициентами и стандартной правой частью.
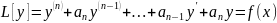 (18)
(18)
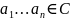
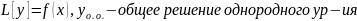
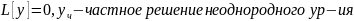
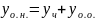
Теорема
10:Пусть
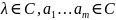 ,
,
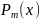 -многочлен
степени m
с комплексными коэффициентами
- характеристический многочлен оператора
L
или ур-ия (18) и
-многочлен
степени m
с комплексными коэффициентами
- характеристический многочлен оператора
L
или ур-ия (18) и
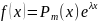
 (19) , Тогда
(19) , Тогда
1)Нерезонансный
случай: Если
не является корнем характеристического
многочлена
то
ур-ие (19) имеет частное решение вида :
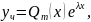 где
где
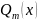 -многочлен
степени m.
-многочлен
степени m.
2)Резонансный
случай:
Если
является корнем кратности x
характеристического многочлена
,
то ур-ие (19) имеет частное решение вида:
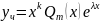 ,
где
-многочлен
степени m.
,
где
-многочлен
степени m.
Док-во(для
случая m=0
т.е.
 ):
):
а)
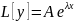 ,
,
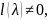

L=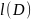 ,
,

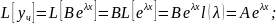
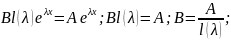
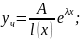
б)
–
корень
кратности k
т.е.
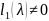
L=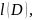
L=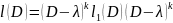
Ищем
частное решение
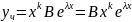 подставим
в ур-ие (19)
подставим
в ур-ие (19)


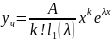
Лемма
6:
Если
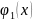 – решение ур-ия
– решение ур-ия
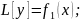
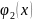 -решение
ур-ия
-решение
ур-ия
 то
то
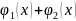 решение ур-ия
решение ур-ия
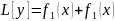
Док-во:По
условию


Лемма
7:Пусть

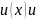
 – действительные функции;
– действительные функции;
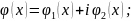
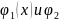 - действительные функции. Если
- действительные функции. Если
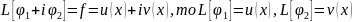
Инструкция:
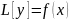 где
где
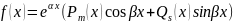

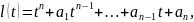
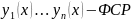
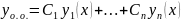 ,
,
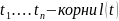
а)


б) – корень кратности k
– корень кратности k
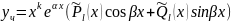
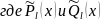 – многочлены
степени l
от x
– многочлены
степени l
от x
22. Нормальная система оду. Понятия решения и интегральной кривой.Постановка задачи Коши для нормальной системы, формулировка тсе.
Опред.: Нормальной системой ОДУ называется система ур-ий вида:

Замечание1: - зависимые переменные от независимой
переменной x
- зависимые переменные от независимой
переменной x
Замечание2:Число ур-ий равно числу зависимых переменных
Замечание3: Порядок системы равен числу ур-ий
Замечание4: Каждое ур-ие ситемы разрешено относительно производной 1-го порядка.Правая часть производных не содержит.
Говорят
что на промежутке I=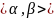 определена вектор-функция
определена вектор-функция
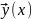 ,
если на I
заданы функции
,
если на I
заданы функции
Векторная
запись системы (1):

Опред.:
Решение
нормальной системы ОДУ (1) назыв-ся
упорядоченный набор функций
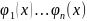 определенных на промежутке I=
и удовлетворяющих условиям:
определенных на промежутке I=
и удовлетворяющих условиям:
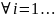 n:
n:
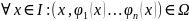
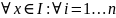
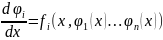
Опред.:Решение
нормальной системы ОДУ (1) назыв-ся
вектор-функция
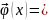 определенная на промежутке I
и удовлетворяющая условиям:
определенная на промежутке I
и удовлетворяющая условиям:
Опред.:
Пусть
решение
системы (1),(2) на промежутке I
кривая
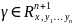 и заданная параметрически уравнениями:
и заданная параметрически уравнениями:
 называется интегральной кривой систем
(1),(2)
называется интегральной кривой систем
(1),(2)

Постановка задачи Коши
Дано:1)Система (1)
2)Точка

Найти:
- решение определенное на окрестности
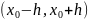 точки
точки
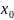 и удовлетворяющая условиям:
и удовлетворяющая условиям:
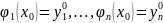 или
или
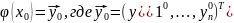
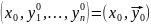 – начальное
условие задачи Коши
– начальное
условие задачи Коши
Запись:

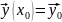
Теорема(ТСЕ1
для нормальной системы ОДУ):Пусть
вектор-функция
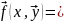 определены и непрерывны в области
определены и непрерывны в области
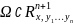 и точка
и точка

Тогда
существует
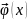 - решение задачи, Коши такое:
- решение задачи, Коши такое:
 ,
определенное на интервале
,
определенное на интервале