6.Обобщенное понятие интегральной кривой.

D 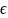|R² Опред.1| Пусть P(x,y) и Q(x,y) непрерывны в обл.D. Кривая γ ={(x,y), x=φ(t), y=ψ(t), t I=< α, β>} называется интегральной кривой ур-я (1)P(x,y)dx+ Q(x,y)dy=0,если выполняются условия:

1) φ(t), ψ(t) С¹(I) 2) 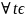I: (φ(t), ψ(t)) D

3) I: P((φ(t), ψ(t)) φ ⁽¹⁾(x)+Q((φ(t), ψ(t)) ψ⁽¹⁾(t)≡0

Опред2| Если интегральная кривая ур-я (1) задаётся в виде Ф(х,у)=0, то это ур-е будем называть интегралом ур-я (1).

Опред3| Уравнение Ф(х,у)=С называется общим интегралом ур-я (1), если1) 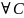: Ф(х,у)=С – интеграл ур-я (1) ;2) Любой интеграл ур-я можно получить подбором соответствующих произвольныз постоянных С.

Ур-е в полных дифференциалах: Пусть P(x,y) и Q(x,y) С¹(D), ур-е P(x,y)dx+ Q(x,y)dy=0 называется ур-ем в полных дифференциалах ,если 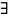U(x,y) С¹(D), такая что dU(x,y)= P(x,y)dx+ Q(x,y)dy

(2) dU(x,y)= P(x,y)dx+ Q(x,y)dy=0, ясно что dU(x,y)= 0 U(x,y)=С. Докажем что U(x,y)=С – общий интеграл ур-я(2): пусть γ ={(x,y), x=х(t), y=у(t), t I=< α, β>}- интегральная кривая(2) P(x(t),y(t))x⁽¹⁾_tdx+ Q(x(t),y(t))y⁽¹⁾_tdy=0= dU(x(t),y(t)) – т.е существует С |R такое что 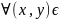γ: U(x,y)=C

7.Уравнения первого порядка, не разрешенные относительно производной.

Пусть в обл. в G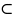 |R³_х,у,р опред. непр. Функция F(x,y,p) и ур-е F(x,y,p)=0 имеет хотя бы 1 решение в обл. G. Говорят,что урав. F(x,y,p)=0 задает в обл. D |R²_x,y функцию p=f(x,y),если:1) (x,y)ϵD: ((x,y),f(x,y))ϵG. 2) (x,y)ϵD: F(x,y,f(x,y))≡G. В этом случае p=f(x,y) неявно задается ур-ем F(x,y,p)=0.

Рассмотрим функцию F(x,y,U₁) опред. на G |R³. (1) F(x,y,у⁽¹⁾)=0 ур-е 1ого порядка неразреш. отн. производной.

Постановка задачи Коши: Пусть F(x,y,p) опред.в обл. в G |R³_х,у,р , точка(х₀,у₀,р₀)ϵ G и F(x,y,p)=0. Найти φ(x)решение ур-я F(x,y,p)=0 оперд. на некотор. окрестности (х-h,x+h)точки х₀ и уд. усл. φ(x₀)=у₀, φ⁽¹⁾(х₀) =р(х₀). Запись задачи Коши: F(x,y,у⁽¹⁾)=0, у(х₀) =у₀ у⁽¹⁾(х₀) =у⁽¹⁾₀, где F(x₀,y₀,у⁽¹⁾₀)=0

Опред| Решение ур-я F(x,y,у⁽¹⁾)=0, через каждую точку которого, проходит ещё одно решение, касаясь того же направления, называется особым решением

8.Общий метод введения параметра.

F(x,y,у⁽¹⁾)=0 ур-е 1ого порядка неразреш. отн. производной. Будем искать решение (интегральную кривую) в параметрическом виде(2) γ {х=х(р), у=у(р), рϵ < α, β>. Вводим параметр у⁽¹⁾=р. Сводим уравнение к разрешенному отн. производной у=f(x, у⁽¹⁾) или x=g(y, у⁽¹⁾). Решение ищем в виде γ {х=х(р), у=у(р),

γ {х=х(р), у=f(x(р),p), p=p(x), p⁽¹⁾(x)≠0. Рассм. равенство: у=f(x,p) и продиффер. его по х,считая р=р(х); 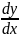= + 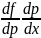т.к = у⁽¹⁾=р. (1)р=f⁽¹⁾_x+f⁽¹⁾_pp⁽¹⁾_x ур-е (1) разреш. отн. произв р⁽¹⁾_х. Т.к р⁽¹⁾_х≠0 и х⁽¹⁾_р=1/р⁽¹⁾_х;

(1*) рх⁽¹⁾_р= х⁽¹⁾_р+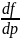 . Решаем (1*), находим х(р), подставляем в (2).

9. Уравнения Лагранжа и Клеро.

Ур-ие Лагранжа: y=f(y’)*x+g(y’) (1); f(y’) ≠y’; y’=p; {x=x(p),y=y(p); {x=x(p),y=f(p)*x+g(p); y_x’=f(p)+x*df/dp* p_x’+dg/dp* p_x’; p-f(p)=x*df/dp* p_x’+dg/dp* p_x’; Если p-f(p) ≠0 и т.к. p_x’≠0; (p-f(p))* x_p’=x*df/dp+dg/dp лин. ур-ие относит. x(p). Если сущ-ет p₀

такое, что f(p₀)= p₀=0, т.е. f(p₀)= p₀

то ур-ие (1) имеет реш-ие вида; y=f(p₀)+g(p₀) или y= p₀*x+g(p₀));

Ур-ие Клеро: y=x*y’+g(y’)(2); вводим параметр p=y’; {x=x(p), y=x*p+g(p); y_x’=p+x* p_x’+ g_p’*p_x’; p = p + x*p_x’ + g_p’*p_x’; [x + g_p’(p)]*p_x’ = 0; a) p_x’=0 p=c; y=c*x+g(c) семейство прямых( реш ур-ия (2)); б) x+g’(p)=0x=-g’(p); Уравнение интегральной кривой γ : {x = - g’(p); y = - p*g’(p) + g(p); Пусть g(p) ЄC1(I), g’’≠0; в этом случае γ-особая интег-ая кривая(2), пусть p₀Є I : (x₀;y₀) Є γ; { x₀ =-g’(p₀), y₀=- p₀g’(p₀)+g(p₀) Для γ в точке (x₀;y₀) y_x’ - тангенс угла наклона касательной y_x’ (x₀;y₀)= p₀; y=c*x+g(c); {x₀=-g’(p₀), y₀=- p₀*g’(p₀)+g(p₀)=c* x₀+g(c); y_x’(x₀)= p₀=c; c= p₀; реш-ие y= p₀*x+g(p₀) проходит через точку (x₀;y₀) касаясь интегр-ой кривой особая инт-ая кри