39. Исследование устойчивости положения покоя системы двух лду с постоянными коэффициентами в случае .

A= ,

Точки покоя:

,

det(A-λE) = 0

=0 – характеристическое уравнение.

– корни характеристического уравнения.

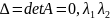=0, пусть .

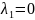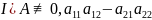=0.

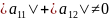
Точек покоя бесконечное множество

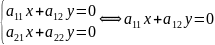
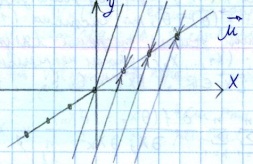
Все точки покоя заполняют прямую

. .

,

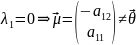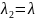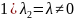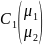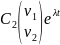= + параметрическое задание прямой с направляющим вектором

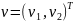
а) все решения ограничены система устойчива.

асимптотической устойчивости нет так как:

б) неустойчивая система

2)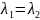 =0

= + ,

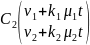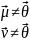
Решение ненулевое неограниченно 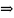система неустойчива.

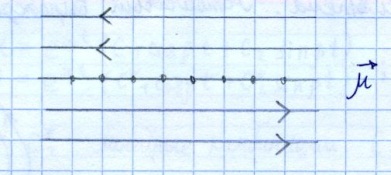
II) A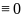 точки покоя - все точки плоскости

40. Нелинейные системы. Исследование устойчивости по первому приближению. Теорема Ляпунова.

dx/dt=f(t,x);(9)

dxi/dt=fi(t,x1…xn); f(t, )= ;

пусть система (9) предст. в виде dx/dt=A(t)x+R(t,x) (10)

где А(t)=aij(t), где aij(t) [t0;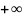 ) выполняется неравенство:

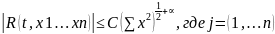
Тогда dx/dt=A(t)x называется системой первого приближения для (9),(10).

Теорема Ляпунова: пусть вектор-функция R(t,x) непрерывно диффер. при 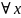(IIxII<C0) и для 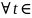[t0; )

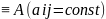а А(t) , тогда 1)если все корни det(A-λE) = 0

имеют отриц. действит. корни, то нулевое решение системы (9) и (10) асимптот. устойчивое. 2)если сущ. Корень характер. уравнения, имеющий положит.действит. числа, то нулевое решение системы неустойчиво. (БЕЗ ДОКАЗАТЕЛЬСТВА)

Теорема. Если вектор-функция f(x) дважды непрерывно диффер. В окрестности точки х=0 и f(0)=0, то система dx/dt=f(x) приводится к виду dx/dt=A(t)x+R(t,x) и для нее справедливы условия теоремы Ляпунова.