1.Понятие дифференциального уравнения, его порядка и решения.

Пусть Ω – область в 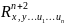и функция F(x,y,u₁…u_n)

Определение 1.Обыкновенные дифференциальные уравнения(ОДУ) называется соотношение вида F (x ,y, y' y" … y⁽ⁿ⁾) =0 , где x – независимая переменная

y=y(x) – функция от (х, y, y' y" … y⁽ⁿ⁾) – производная y(x) n – порядок уравнения

Пример

a) F(x,y,u₁)=f(x,y)-u₁

F(х,y, y')=F(х,y)- y'

F(х,y) – y'=0 y'=F(х,y)

Определение 2.Решением уравнения называется функция y=φ(x) определённая на промежутке I=<α ,β> удовлетворяющие условию

1. Φ(x) ∈Cⁿ(I)

2. ∀x∈I:(x, φ (x), φ' (x) ,…, φⁿ (x)) ∈Ω

3. ∀x∈I:( x, φ (x), φ' (x) ,…, φⁿ (x)) ≡0

Пример 2:Пусть F(x) непрерывна на промежутке [a;b] и y(x) –первообразная F(x)

На [a;b]

Тогда y'(x)= F(x).Это уравнение порядка n=1

y(x)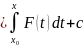 , где x₀∈[a;b]; уравнение имеет бесконечно много решений

Задачи, решаемые теорией ОДУ:

1) Отыскание всех решений ОДУ (то есть общего решения),

2) ОДУ решается с дополнительными условиями:

А) условия Коши,

Б) краевые условия,

В)функциональные условия.

В этом курсе мы будем решать задачу 1 и 2(а).

2.Оду первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения. Постановка задачи Коши.

Пусть область D∈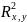 и F(x,y) определена на D y'=F(x,y)

Определение 3. φ(x) определена на промежутке I=<α ,β> называют решением уравнения y'=F(x,y) если:

1. φ(x) ∈C¹(I)

2. ∀x∈I:(x, φ(x))

3. ∀x∈I:φ'(x) ≡F(x, φ(x))

Определение 4. Если y= φ(x) является решением y'=F(x,y),то график этой функции называют интегральной кривой уравнения y'=F(x,y).Ясно ,что интегральная кривая

∈ D

Геометрическая интерпретация

Говорят ,что в области D∈R² задано векторное поле 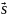,если в каждой точке M(x,y) ∈ В поставлен в соответствии вектор (x,y),приложенный к этой точке

Для уравнения

y'=F(x,y) построено векторное поле

(x,y)= – поле направления

Пусть y= φ(x) интегральная кривая y'=F(x,y),

В точке (x , y)

y'= φ' (x)=F(x, φ(x))=F(x,y)

Т.е тангенс угла наклона к φ= φ(x) равен F(x,y)

Постановка Задачи Коши

Постановка задачи –необходимо понять ,что задано и что надо найти

Дано : В области D заданы дифф.ур-ия y'= F(x,y) и два числа x₀ и y₀ такие ,что (x₀,y₀) ∈D

Найти : решение y= φ(x) уравнения y'=F(x,y) определена на некотором интервале где x₀∈ I=<α ,β> и удовлетворяет условию φ(x₀)=y₀, числа x₀ и y₀ называются начальными условиями.

Условная запись задачи Коши

y'= F(x,y),y(x₀)=y₀

Замечания

1. Если F(x,y) ∈C(D) То задача Коши имеет решение в любой точке в области D

2. Решений у уравнения y'= F(x,y)бесконечно много

3. (x₀,y₀) ∈D:Для единственности решения требует дополнительные условия

3.Формулировка теоремы существования и единственности ( тсе ). Понятие общего решения.

Обобщение некоторых понятий .Пусть f(x,y) определена в области D∈ точка (x₀,y₀) ∈D

Рассматриваем задачу коши

(8)

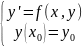
Пусть φ₁(x) и φ₂(x) решения (8),т.е φ₁(x) ,φ₂(x) - решение y'=F(x,y),

φ₁(x₀)=y₀

φ₂(x₀)=y₀

Определение 5.Говорят ,что задача Коши (8) имеет единственное решение если любые два решения φ₁(x) и φ₂(x) этой задачи ,совпадают на некоторой окрестности точки x₀ т.е ∃ δ>0∀x∈( x₀ – δ, x₀ +δ): φ₁(x) ≡ φ₂(x)

ТеоремаТСЕ1(локальная)

Пусть на области D∈ функция 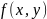и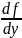 (x,y) определена и непрерывна и точка (x₀,y₀) ∈D .Тогда уравнение 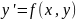имеет решение φ(x)

1)Определена на некоторой окрестности ( x₀ – h, x₀ +h) точки x₀ , удовлетворяет условию

φ(x₀ )= y₀

2)Такое решение единственное(Без док-ва)

Замечание к ТСЕ

Пусть в D выполняется условие ТСЕ1

1)В D бесконечно много решений уравнения, x₀ - точка (x₀ , y₀) ∈D.Через эту точку проходит единственное решение y=φ(x₀ , y₀).Все эти решения не совпадают

Определение 6. Пусть удоволитворяет в D условием ТСЕ1

Функция y=φ(x,C) называют общем решением y'= F(x,y) в области D,если

1. ∀C: φ(x,C) решением φ(x,C)

2. Любое частное решение y'=F(x,y) может быть получен из φ(x,C) подбором соответствующего значения C

2⁰ Решением задачи может быть определена лишь на некоторой (небольшой ) окрестности точки x₀