3.Вычисление проекции вектора на направление другого вектора.(выразить проекцию из

, или  .)

4)Вычисление длины вектора в произвольном базисе.

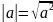
5) a перпендикулярен b 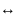a*b=0

12.Векторное произведения векторов. Свойства и выражение в декартовых координатах.

Векторным произведением вектора   на вектор   называется вектор, обозначаемый символом   и определяемый следующими тремя условиями:

1). Модуль вектора   равен  , где   - угол между векторами   и  ;

2). Вектор   перпендикулярен к каждому из вектора   и  ;

3). Направление вектора   соответствует «правилу правой руки». Это означает, что если векторы  ,   и   приведены к общему началу, то вектор   должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору  ), а указательный - по второму (то есть по вектору  ).

Векторное произведение зависит от порядка сомножителей, именно:

.

Модуль векторного произведения   равен площади S параллелограмма, построенного на векторах   и  :

.

Само векторное произведение может быть выражено формулой

,

где   - орт векторного произведения.

Векторное произведение   обращается в нуль тогда и только тогда, когда векторы   и   коллинеарны. В частности,  .

Если система координатных осей правая и векторы   и   заданы в этой системе своими координатами:

,  ,

то векторное произведение вектора   на вектор   определяется формулой

,

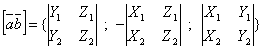или

.

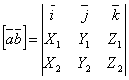Свойства:

1.a*b=-b*a.

2.a*b=0 a || b

3.(£*a)*b=£*(a*b)

4.(a+b)*c=a*c+b*c

Применение:

1)Вычисление момента силы F приложенной в точку A относительно точки O:

M=OA(вектор)*F

2)Вычисление площадей параллелограмма и треугольника построенных на векторах a и b:4

S(паралг)=

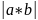
S(треуг)=1/2*

4)Условие компланарности векторов: a || b a*b=0

13.Смешанное произведение векторов. Свойства и выражение в декартовых координатах.

Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись  ,  ,   означает, что вектор   считается первым,   - вторым,   - третьим.

Тройка некомпланарных векторов  ,  ,   называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы  ,  ,   расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов  ,  ,   называется число, равное векторному произведению  , умноженному скалярно на вектор  , то есть  .

Имеет место тождество , ввиду чего для обозначения смешанного произведения   употребляется более простой символ  . Таким образом,

,  .

Смешанное произведение   равно объему параллелепипеда, построенного на векторах  ,  ,  , взятого со знаком плюс, если тройка   правая, и со знаком минус, если эта тройка левая. Если векторы  ,  ,   компланарны (и только в этом случае), смешанное произведение   равно нулю; иначе говоря, равенство

есть необходимое и достаточное условие компланарности векторов  ,  ,  .

Если векторы  ,  ,   заданы своими координатами:

,  ,  ,

то смешанное произведение   определяется формулой

.

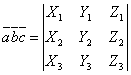Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов  ,  ,  ).

Свойства:

1) когда все три вектора компланарны. Не являются базисными векторами.

2) (при перестановке двух соседних векторов меняется знак).

3)При циклической перестановке смешанное произведение не меняется.

4).

Приенение :

1)V(параллелипипида)=|a*b*c|

2)V(пирамиды)=1/6*|a*b*c|