9.Понятие вектора. Линейные операции над векторами . Понятие базиса. Координаты вектора. Проекция вектора на ось.

Вектор- направленный отрезок прямой имеющий начало и конец.

Модуль вектора – это его длина.(расстояние между началом и концом).

Нулевой вектор – его длина=0(не имеет направления(точка)).

Векторы   и  , расположенные на одной  прямой или на параллельных прямых, называются коллинеарными. 

Нулевой вектор коллинеарен любому вектору.  Два вектора   и   называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.  В этом случае пишут  . 

Два коллинеарных вектора (отличные от  нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными. _  Вектор, противоположный вектору  ,  обозначается  .  Для вектора   противоположным является вектор  .  

Линейные операции над векторами.

1.Сложение векторов.

а)Правило треугольника.

б)Правило параллелограмма.

2.Разность векторов а и б называется такой вектор с, что а=б+с.

3.Умножение вектора на число:

Произведением вектора   на число   называется вектор б , который:

1. коллинеарен вектору  ;

2. сонаправлен ему, если 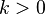 , или противоположнонаправлен, если  ;

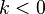3. длины связаны следующим соотношением:  .

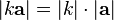Замечание: всякий вектор – это произведение его модуля на орт.

Линейная комбинация векторов   с коэффициентами   — вектор  . Если все коэффициенты равны нулю, линейную комбинацию называют тривиальной, иначе — нетривиальной.

Векторы   называются линейно зависимыми, если существует их нетривиальная комбинация, равная нулю.

Теорема

Система векторов линейно зависима тогда и только тогда, когда один из векторов является линейной комбинацией остальных.

Доказательство  [скрыть]

Необходимость. Пусть система векторов линейно зависима. Это значит, что существует нетривиальная линейная комбинация, равная нулю:  . Один из коэффициентов, например   не равен нулю. Тогда

Достаточность. Пусть  . Тогда

Это нетривиальная (коэффициент  ) линейная комбинация, равная нулю. Значит система векторов линейно зависима.

Геометрический смысл линейной зависимости заключается в следующем:

1. система из двух векторов линейно зависима тогда и только тогда, когда векторы коллинеарны;

2. система из трех векторов линейно зависима тогда и только тогда, когда векторы компланарны;

3. всякие четыре вектора линейно зависимы.

Понятие базиса.

Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства по ней раскладывается

Любой декартовой системе координат на плоскости или в трехмерном пространстве (также и в пространстве другой размерности) может быть сопоставлен базис, состоящий из векторов, каждый из которых направлен вдоль своей координатной оси. Это относится и к прямоугольным декартовым координатам (тогда соответствующий базис называется ортогональным), так и к косоугольным декартовым координатам (которым будет соответствовать неортогональный базис).

Часто удобно выбрать длину (норму) каждого из базисных векторов единичной, такой базис называется нормированным.

Наиболее часто базис выбирают ортогональным и нормированным одновременно, тогда он называется ортонормированным.

В любом векторном пространстве базис можно выбрать различным образом (поменяв направления его векторов или их длины, например).